Casi clinici 5
Prima parte
“Arieggiare, dare aria”.
Una metafora. Piste indiziarie.
1. Le righe seguenti possono essere considerate sotto la metafora della finestra. 1.1 Cosa é la finestra? La cornice che la contiene o l’apertura contenuta, con eventualmente tutto l’orizzonte che ne può trasparire? Per finestra, il dizionario considera l’apertura praticata in un muro, il parlar comune dice “apri la finestra”, così da arieggiare un locale. Il dizionario, per finestra, considera però pure i battenti, le persiane. Ma se il muratore dice “ho fatto un’apertura”, nel senso di aver aperto una finestra, pure il falegname dice ho “fatto una finestra”, nel senso di averla sagomata oppure posata … Insomma supporto fisico, intelaiatura, o vuoto spazio che da su di un orizzonte … con finestra intendiamo molte cose differenti fra loro.
1.2 … insomma tratterò di due cose: di esecuzione, di posa, … e di sguardo. Eseguire una finestra, posare una finestra, guardare oltre la finestra. Questi gli oggetti cognitivi di queste riflessioni. Da un lato tratteremo di tecniche, di meccaniche; tratteremo di elementi esecutivi e di elaborati manuali o fisici, di algoritmi ripetuti e ripetibili. Dall’altro tratteremo di logiche e di rappresentazioni, di pensieri, di narrazioni, di sguardi …
1.3 Certamente, necessitiamo dell’esecuzione e della posa della finestra per poter guardare oltr’essa. Senza finestra non ci sarebbe sguardo che la travalica. A scuola si tratta di saper fare tutte e tre le cose: eseguire, posare, guardare.
Ma si contempla l’intelaiatura o l’orizzonte?
1.4 Certamente, si può anche contemplare una bella intelaiatura. L’algoritmo come opera d’arte …
Ma se le competenze esecutive diventano imperio? Purtroppo le pedagogie della padronanza, oggi, sembrano aver raccolto il suggerimento alla scuola di farsi azienda. Luogo di gestione “ottimizzata” della complessità e della diversità dei bambini, diversità di ritmi, esperienze, culture, eccetera. Apparati didattici differenziati quali strumenti anestetici delle differenze. L’insensibilità alle differenze individuali (al bambino soggetto) si esplica nella gestione tutta operatoria delle stesse …
Seconda parte
Osservazioni
Organizzazioni e rappresentazioni del sapere, organizzazione e rappresentazione del pensiero
1 A scuola, come ci si pone la questione dell’oggetto dell’apprendimento, l’oggetto cognitivo – che sia una materia scientifica, dei saper fare, degli algoritmi?
1.1 E come viene considerata, a scuola, la posizione dell’allievo dirimpetto l’oggetto di apprendimento così definito?
1.1.1 L’allievo come si rappresenterà ed organizzerà una conoscenza?
2 Ecco. Qui comincia l’osservazione e la descrizione di un intervento di sostegno. L’osservazione di un paesaggio didattico, di una campo di lavoro con la sua organizzazione, la descrizione di un processo “epigenetico”. Processo svolto da un allievo utente del servizio di sostegno. Dopo un richiamo rapido della natura del materiale differenziato concreto, vedremo come il bambino é arrivato ad organizzare e quindi a concepire la sua “materia di apprendimento”. In questo caso la matematica in quarta elementare.
3 DIMAT é organizzato secondo un livello di difficoltà crescente. 21 sono gli argomenti presentati, dalla conoscenza del numero, alle operazioni, alle misure e ai diagrammi. La materia é suddivisa in tre livelli per ogni argomento. I 21 argomenti così suddivisi danno 63 schede. Classificate secondo tre criteri: ognuna con un numero progressivo e la doppia indicazione del livello e dell’argomento. Sono accompagnate da consegne esecutive e qualche volta da commenti che portano l’allievo a prestare attenzione a qualche cosa in particolare. Il testo é ridotto al minimo. L’allievo lavora in maniera individualizzata, su un percorso del tutto personale. Momenti di lezioni frontali, o attività a gruppi sono integrate idealmente a momenti di esercitazione individualizzata. Purtroppo con classi molto numerose lo spazio per delle relazioni d’insegnamento-apprendimento dirette tra docente ed allievo sono ridotte. Così, in classe la relazione di precettorato (modello che sta alla base teorica ed ideale degli insegnamenti individualizzati) si frammenta in molteplici micro interventi regolatori. In classe, preciso e sottolineo, in determinate classi, la differenziazione viene quindi ad essere organizzata per lo più secondo uno stile neo-cognitivista, dominato dalle catene stimolo risposta. Ove lo stimolo é quello di riuscire la verifica. Ove l’ideale della relazione di precettorato – che sta un po’ alla base dei percorsi didattici personalizzati ed individualizzati a seconda dei ritmi d’apprendimento degli allievi – non é possibile. Il precettorato si realizza in una relazione contrattuale individuale e non di un docente con una classe.
4 Mi dico:
– 1) se do tutto il materiale – lo schedario completo – in disordine,
– 2) se tolgo tutte le indicazioni classificatorie, titoletti, sigle che indicano l’appartenenza della scheda ad un argomento piuttosto che ad un altro, indicazioni che permettono di raccogliere e suddividere le schede in argomenti distinti e classarle negli appositi scomparti del raccoglitore, vale a dire se tolgo tutta la segnaletica, vale a dire tutti gli indizi, le marche, chiamiamole come vogliamo, che indicano sia l’argomento trattato come pure il luogo della sua classificazione, se tolgo tutto ciò …
lasciando tutto il resto, le consegne, i calcoli ecc … insomma tutto quanto é di operativo nell’esecuzione della scheda e nella comprensione della sua natura, in poche parole se spoglio il materiale degli indizi che ne indicano l’organizzazione, un allievo come raccoglierà il materiale, quali gruppi opererà ? Come lo organizzerà? Mi dico: se l’ha già sperimentato per un anno, qualcosa di quell’organizzazione rimarrà, in seguito. L’ordine che ne farà il bambino in qualche maniera sarà analogo all’organizzazione originaria. Non penso propriamente ad una fotocopia totalmente aderente all’organizzazione originale. Però penso che organizzerà tutto lo schedario secondo criteri analoghi a quelli sperimentati l’anno precedente. Penso: la rappresentazione che si farà del materiale che gli proporremo non sarà del tutto spontanea. Anzi, si suppone che segua il percorso già effettuato l’anno precedente e quindi ne ripercorra l’organizzazione sperimentata. La “lettura”, intesa come comprensione, come cognizione, ovverosia come pensiero, che si farà del materiale, sarà mediata da quanto già sperimentato lungamente sui banchi di scuola. Invece, …
5 Che sia ben chiaro non tratto della padronanza degli algoritmi, della acquisizione delle tecniche di calcolo o computazionali: – parlo di rappresentazioni della matematica, – parlo di organizzazione della matematica, – parlo di padronanza dei concetti e di padronanza degli obiettivi.
6 Trattiamo di un bambino di quarta elementare, che quindi ha già avuto modo di lavorare con questo approccio differenziato durante un anno. Conosce DIMAT, il suo principio organizzativo differenziato e per livelli di difficoltà, se non altro almeno per averlo sperimentato durante l’anno scolastico precedente. La ri-organizzazione delle schede da parte del bambino ha richiesto parecchie sedute di lavoro. A un primo raggruppamento del tutto spontaneo ne é seguito un altro “mediato” dal sottoscritto che ha avuto inizio da una mia suggestione e richiesta Riporto qui i raggruppamenti così ottenuti, senza indicare il lavoro successivo. Lavoro che é consistito nella costruzione, passo a passo, di un sistema organizzato, logico-matematico, coerente del materiale. Un metodo che prevedeva costanti confronti e raggruppamenti, argomentati, di costruzione di classi e sotto classi di “oggetti” di conoscenza. Un lavoro molto metacognitivo, in un certo senso inspirato ad una didattica costruttivista, con particolare attenzione a 2 caratteristiche del pensiero operatorio: la reversibilità e l’osservazione (auto-osservazione) dell’azione. Qui ci interessa il modo di considerare la materia scolastica (qui la matematica, in particolare Dimat). Non tratterò quindi del lavoro di rieducazione svolto in seguito. Riporterò solo la rappresentazione del materiale (concretamente fornita dalla organizzazione del materiale del bambino).
Prima organizzazione
Il lavoro comincia così. Dico: “senti un po’ bambino, guarda un po’. E’ successo un pasticcio tipografico. Quest’anno si sono dimenticati di stampare le schede come si deve. Vedi, qui e qui (indico con le dita) non c’é scritto di cosa si tratta … E poi guarda tutte le schede, me le hanno date in disordine. Ti ricordi lo scorso anno? Le schede le avete messe tutte nel classificatore, ben ordinate che si poteva sapere? E adesso che facciamo?”.
Il primo raggruppamento eseguito dal bambino é piuttosto semplice. Basato su indizi percettivi di facile reperimento, quali le indicazioni del livello di difficoltà delle schede. Così opera 3 primi raggruppamenti:
– tutte le schede F (facili)
– tutte le schede M (medie)
– tutte le schede D (difficili)
ai quali ne associa poi altri due
– le schede che presentano due livelli di difficoltà F + M
– le schede che presentano tre livelli di difficoltà F + M + D.
Quale ipotesi di ragionamento ne possiamo dedurre? 1) Ecco, la prima cosa che salta all’occhio, è della sorta di un corto circuito. In verità il materiale proposto si presenta come una tabella a doppia entrata (vedi tabella entrata allegato A). All’ascissa i contenuti matematici, gli argomenti da affrontare, e all’ordinata il livello di difficoltà. Il bambino, invece di ripercorre questa doppia classificazione, salta tutta la parte qualitativa, tutta la parte in comprensione, per ritenere solo quella in estensione. Là dove per comprensione consideriamo la varietà delle caratteristiche o informazioni, contenute in un concetto, e dove per estensione consideriamo il numero dei casi particolari che rientrano in un concetto. In verità la sua non è una operazione mentale, è un agire poco differenziato, dell’ordine percettivo, poco operatorio, un agire che fa della lettura un’attività di riconoscimento di segnali percettivi ma non di comprensione. Certamente possiamo già chiederci quali competenze classificatore possiede, Spontaneamente, senza la successiva stimolazione mia, sembrano essere solo sequenziali. Un corto circuito banale, quanto inaspettato. Solo in seguito (come vedremo) tramite induzione appare una necessità di maggiore organizzazione.
2) la comprensione della matematica in primo luogo é mediata dalla sua esecutività: i livelli. La matematica? Insomma é una roba da eseguire, prima i “F”, i facili, poi i “M”, i medi, poi i “D”, i difficili. Per il resto non c’è molta attenzione. Siamo in un contesto decisamente poco operatorio; poco pensiero matematico é presente in questo considerare l’ordine delle cose matematiche. La matematica non é un oggetto di pensiero, non é un sistema di organizzazione del mondo e quindi una conoscenza. La matematica é l’esecuzione autonoma di algoritmi. Una forte dipendenza dal campo, appare qui, altro che autonomia.
3) Siamo su un registro percettivo motorio, o senso motorio. Percettivo (e potremmo pure dire grezzo) perché basato su indizi poco pertinenti riguardanti l’operatività cognitiva. Motorio, perché quei pochi indizi scaturiscono da una esperienza già fatta che é quella della classificazione delle schede in appositi scompartimenti del classificatore.
La domanda fin troppo facile è: dove sta il pensiero logico-matematico? Dove stanno l’osservazione, il confronto, la classificazione e la differenziazione? Dove stanno le proprietà delle operazioni? In verità questo tipo di organizzazione “spontanea” é molto funzionale ad un registro della matematica sperimentata su vettori esecutivi, percettivo motori o senso motori. Con questo registro lo sforzo principale è diretto all’acquisizione degli algoritmi, esercitati nell’esercitazione “circolare” di schede, come espletazione di procedure (espletare = fare il proprio dovere) …
Siamo nel regno delle reazioni circolari primarie e secondarie.
Prendo a prestito una nozione che d’abitudine in psicologia siamo abituati a considerare nei primi mesi di età. In verità questa si può benissimo applicare all’apprendimento e alla esercitazione degli algoritmi aritmetici. Reazioni circolari primarie: tra il primo e il quarto mese di vita il bambino sviluppa le reazioni circolari primarie ovvero la ripetizione di un’azione casuale per ritrovarne gli effetti gradevoli. L’esempio è la suzione del dito, trovandola piacevole il bambino la ripete per lunghi periodi. Reazioni circolari secondarie: tra il quarto mese e l’anno di vita il bambino orienta i suoi comportamenti verso l’ambiente esterno cercando di afferrare e muovere gli oggetti e osserva i risultati delle sue azioni. Agitando un sonaglio provoca dei rumori piacevoli e cerca di ripetere l’azione per riprodurre il suono. Reazioni circolari differite:tra gli 8 e i 12 mesi il bambino è in grado di riprendere un’azione su un oggetto dopo averla interrotta. Reazioni circolari terziarie: dai 12 ai 18 mesi. Consistono nello stesso meccanismo descritto in precedenza ma effettuato con variazioni attive. Ad esempio afferrare e battere un oggetto contro superfici diverse. In questa fase il bambino inizia a comprendere la permanenza degli oggetti mentre nelle fasi precedenti se l’oggetto non è in vista “non esiste”.
L’interazione del bambino con il suo oggetto di conoscenza si attua piuttosto sul registro delle imitazioni procedurali che non sulla assimilazione di concetti, sulla assimilazione di proprietà.
4) Siamo in un registro dell’ordine del fare, dell’eseguire secondo canali, schemi e strutture eterodiretti. Schemi e strutture d ripetere ed acquisire. Un registro dell’ordine dell’imperativo: “si deve fare” (un registro che nel peggior dei casi cade nell’ordine coattivo e persecutorio, quando l’algoritmo non venendo automatizzato deve essere ripetuto infinite volte, con le buone o le cattive …).
Insomma é interessante, di fronte ad un problema complesso quale quello classificatorio la risposta é molto “ottimizzata”: rapida, esecutiva, quasi immediata, passa subito all’atto, funziona, mette in moto il bambino … La prima risposta é piuttosto dell’ordine del fare che non dell’ordine del pensare.
5) Le modalità di fare che questo bambino propone interrogano due temi fondamentali. Uno, di ordine psicologico ed evolutivo, tratta del rapporto che intercorre fra pensiero senso-motorio e pensiero operatorio. Il secondo di ordine pedagogico didattico interroga la metodologia reale, concreta e quotidiana che i docenti propongono nel loro insegnamento.
Fra:
– maniera di considerare il passaggio ed il rapporto fra pensiero senso-motorio e pensiero operatorio e
– quotidianità didattica c’é una totale interdipendenza. Che questa sia esplicita od implicita.
Seconda organizzazione
Dopo questo primo approccio dico al bambino che, “insomma, quanto tu hai fatto non é male così abbiamo 5 argomenti e sappiamo dove cominciare per prima”. Però … però se pensiamo bene allo scorso anno non so se va veramente bene, intendo dire … se va veramente del tutto bene, ma proprio del tutto. Ti ricordi c’erano molti più argomenti …”.
Qui di seguito appaiono i 23 raggruppamenti successivi che il bambino ha effettuato. Numerati da 1 a 23 con le relative argomentazioni classificatorie da lui espresse.
E’ da ricordare che riporto qui di seguito solo l’esito finale dei raggruppamenti delle schede. Esito di un lungo impegnato lavoro di osservazione, confronto e assemblamenti successivi …
1) “Vanno assieme perché hanno i canguri”. Una scheda d’addizioni e due di sottrazioni sono mescolate dal bambino in una categoria che subito ce la dice lunga sull’approccio figurale o percettivo…
2) “Vanno assieme perché hanno le farfalle e il rotondo”. Tre schede d’addizioni mentali.
3) “Vanno assieme perché hanno le farfalle e hanno il quadrato” Tre schede di sottrazioni mentali.
4) “Questi fogli vanno sono uguali perché ci sono … (senza dirne il nome indica delle colonnine) … le righe e hanno i numeri sotto”. In verità mescola due argomenti: frazioni e diagrammi.
5) “Gli orologi”. Nota, non definisce le misure di tempo. Gruppo che lo mette in crisi perché non riesce a trovare la terza scheda.
6) “Vanno assieme perché c’è scritto misura”. Tre schede di misure di lunghezza. Da notare il riferimento misura.
7) “Vanno assieme perché c’è scritto misura …”. Mette due schede di misure di peso con una di misura di valore! Solo in seguito cercando le tre schede di misure di valore si accorge della incongruenza.
8) “Vanno assieme perché c’è scritto Fr. (franchi)” Tre schede di misure di valore
9) “Vanno assieme perché hanno dei numeri, c’è scritto mille, milione, miliardo. E poi hanno in basso a 10, a 10, a 10” Tre schede di conoscenza dei numeri, che in verità presentano numeri solo sino al 10000. Schede che in basso riportano una tabellina di autovalutazione misurata da 1 a 10.
10) “Vanno assieme perché c’è uguale, maggiore, minore”. Tre schede di conoscenza dei segni aritmetici.
11) “Vanno assieme perché hanno la mano”. Tre schede di sottrazioni scritte.
12) “Vanno assieme perché hanno il per”. Due schede! Una di caselline, una con la tabellina del diviso. In verità le schede di caselline con i calcoli a due o tre cifre (60 x 8, 400 x 5), non fanno parte delle caselline!
13) “Vanno assieme perché hanno le farfalle e il diviso”. Elementi pertinenti e altri figurali mescolati. Due schede di divisione orale.
14) “I giorni”. Una scheda di misure di tempo.
15) “Vanno assieme perché c’è scritto recipiente”. Ecco che si è fatta avanti la necessità di leggere per meglio cogliere la specificità delle schede. Peccato che mescola tre schede di misure di capacità con una di frazioni.
16) “Vanno assieme perché hanno i cerchi con i calcoli”. Intende le addizioni delle tre schede di “addizioni scritte”.
17) “Vanno assieme perché hanno il quadrato con dentro i calcoli”. Tre schede di moltiplicazioni scritte.
18) “Hanno il per”. Tre schede di caselline, due orali, una mentale.
19) “Hanno il diviso” Tre schede di divisione. Una scritta, una mentale, una orale. 20) “Hanno il più”. Due schede di addizione mentale.
21) “Hanno ancora il diviso” Altre tre schede, due di divisione scritta e una mentale.
22) “Vanno assieme perché c’è scritto indica”. Due schede di digrammi.
23) “Queste non so dove metterle, mi rimangono”.
Vediamo di commentare anche queste ultime 23 categorie.
1) Fondamentalmente, possiamo affermare che la veste tipografica delle schede, vale a dire il vestito che presentano, la loro presentazione figurale, fatta di consegne, numeri, cifre, figure, testi accompagnatori, e così via, ebbene la veste tipografica porta degli elementi che portano decisamente fuori strada il bambino.
In effetti là dove ci sono dei disegnini, che nulla centrano con i concetti presentati (farfalle, canguri o altro), il bambino tende a subirne il “fascino” ed effettua tendenzialmente raggruppamenti figurali.
Da notare che l’allievo non riesce a mantenere nemmeno la rigorosa suddivisione per livelli, F, M, D. E l’allievo cade in crisi quando non può mettere tre schede assieme senza sapere come risolvere la contraddizione.
2) Pur mantenendo una forte valenza percettiva-motoria il bambino mette in atto alcune proposte che mostrano lo svelarsi di uno sforzo logico-classificatorio di tipo concettuale. Questo quando la presenza degli stimoli percettivi viene a perdere la sua forza, ovverosia sono ridotti quantitativamente e qualitativamente.
Così accanto ai raggruppamenti figurali appare l’attenzione rivolta ad elementi di maggiore pertinenza aritmetica. Così fra le prime classi di schede che l’allievo cerca di formar vi sono quelle relative alle 4 operazioni aritmetiche, anche se non differenziate nelle loro varietà orale, mentale e scritta. Oppure coglie vari elementi che indicano una pertinenza concettuale: le misure, i segni aritmetici, …
Ciò indica che il tentativo didattico attuato, tentativo mirato alla comprensione della materia matematica, ha una sua legittimità e una sua utilità.
Non deve meravigliare l’assenza di titoli precisi, di “categorie logiche socializzate”, esempio “conoscenza dei numeri”, “segni aritmetici”, “diagrammi”, addizioni scritte”, sottrazioni orali. Non si pretende tanto. Però intanto si vede che l’anno di lavoro scolastico precedente non ha portato a nessuna permanenza di quelle categorie. Meraviglia piuttosto che nessuna categoria sia riuscita a farsi luce in maniera spontanea. Meraviglia che nelle rappresentazioni dell’allievo non ci sia posto per le categorie concrete di un materiale già sperimentato per un anno scolastico. Nota bene, non di un materiale nuovo e sconosciuto.
Là dove i raggruppamenti proposti corrispondono con quelli originari, dove trovarne la ragione? Forse che il bambino ha saputo cogliere l’organizzazione dello schedario matematico e ha saputo differenziare gli argomenti? Come per esempio per il 16° e il 17° raggruppamento? Oppure tali raggruppamenti funzionano perché c’è sempre qualche elemento figurale che distingue un argomento dall’altro? Se la risposta corretta fosse solo la prima, male si capirebbero i gruppi spuri, gli errori, il non rispetto della rigorosa organizzazione in tre livelli, la mescolanza di operazioni diverse in medesimi raggruppamenti e così via. In verità nel 16° e il 17° raggruppamento il bambino manco si è accorto che ci sono due operatori – l’addizione e la sottrazione – scritti. Questo bambino non sa cosa siano l’addizione e la sottrazione, sa cosa è il più e cosa è il per (vedi argomento 18).
3) Una delle ipotesi che regge molte proposte didattiche matematiche è quella di ridurre il linguaggio quanto più possibile, “per favorire quegli allievi che hanno una cattiva padronanza della lettura. Per facilitarli togliamo quindi quante consegne più possiamo in lingua scritta”. Ma una lettura così semplificata aiuta poi veramente lo sviluppo di concetti o spinge ancor più alla pura esecutività? Ad un affidarsi al campo percettivo?
Certamente, ancora una volta si mescolano le carte. Si mette sullo stesso piano la difficoltà delle decodifica di un testo, ovverosia la difficoltà di lettura, con la difficoltà della comprensione di una operazione. Con quei bambini in difficoltà di lettura, ma non di ragionamento, basterebbe leggere le consegne al loro posto per veder risolta la scheda.
Una questione é la difficoltà tecnica di decodifica di un testo, dovuta essenzialmente alla lentezza della lettura, una altra questione è passare da una codifica di una situazione, dal testo dunque, a un’altra codifica, che sia iconica, simbolica o interiore.
Con tutto ciò non c’è da meravigliarsi se rimane forte la pulsione originaria dell’allievo a ordinare il materiale semplificandone la lettura!
Non si aiuta l’allievo debole in lettura (lento, dislessico, o che sia) riducendo le occasioni di pensiero! Che si venga a contrabbandare la dislessia con l’afasia o l’agnosia è il rischio che si propone ignorando il linguaggio in matematica, appunto riducendone il testo nelle schede.
La riduzione del testo é proprio funzionale al riflesso esecutivo.
4) Appare qui in tutta la sua dirompenza lo iato tra rappresentazione ed organizzazione spontanea di un oggetto di conoscenza (lo schedario di matematica) e la sua organizzazione concreta, data da docenti. In verità solo raramente assistiamo a delle didattiche che:
– portino gli allievi a riflettere sull’organizzazione del materiale.
Questa riflessione non può nemmeno poi essere fata una volta e poi basta. Richiede delle riprese, tenuto conto del fatto che siamo in età evolutiva, quindi le rappresentazioni degli allievi vanno modificandosi ad ogni nuova conquista operatoria o ad ogni nuovo stadio cognitivo;
– portino gli allievi a riflettere sui legami fra gli argomenti.
La logica classificatoria proposta in DIMAT con questo bambino è stata poco generalizzatrice. Se si tratta di differenziare gli argomenti fra loro, dando ad ognuno un suo posto ed una sua identità, si tratta di vedere cosa li accomuna e cosa permette di passare da una scheda all’altra, per esempio dalla scheda 2M (segni aritmetici) alla scheda 17M (misure di peso), si tratta di sviluppare delle generalizzazioni;
– presentino agli allievi la matematica nell’insieme delle proprietà delle operazioni aritmetiche (commutativa, associativa, invariantiva, distributiva) e che facciano della padronanza e comprensione di queste proprietà il centro dell’approccio didattico.
In verità l’organizzazione di uno schedario è il compimento di un percorso cognitivo. Percorso effettuato dai suoi autori. Ma all’allievo viene dato come punto di partenza, con quanto meno linguaggio possibile.
5) Con una attività specifica è possibile abbozzare un percorso cognitivo. Percorso che ha permesso al bambino di sperimentare ed osservare le sue contraddittorie ipotesi, i suoi differenti paradigmi di percezione e rappresentazione, quindi di cercare e formulare delle nuove risposte. La registrazione sistematica del suo lavoro gli ha permesso di passare dalla osservazione del materiale alla osservazione di se stesso, veicolata ben inteso sull’osservazione delle proprie realizzazioni.
Terza parte
Indagini
1 L’esposizione precedente è partita da una prima semplice empirica osservazione. Osservazione dettata dalla esperienza quotidiana. L’allievo ha una rappresentazione dei materiali didattici non corrispondente all’organizzazione reale degli stessi. L’allievo, della materia da apprendere, ha una cognizione che non soddisfa appieno le intenzioni di un apprendimento e di un insegnamento disciplinare operatorio.
Le rappresentazioni e la cognizione dell’allievo solo occasionalmente corrispondono agli obiettivi d’insegnamento.
Tratto di conoscenze disciplinari e di conoscenze “trasversali”; tratto di algoritmi, di percezione e cognizione di un compito. Tratto di conoscenza e padronanza di una materia e della organizzazione dei suoi contenuti.
Ciò ha comportato una prima pista di riflessioni, rapidamente proiettatasi a vari livelli sempre allargati
2.1 prima indagine
La prima idea é appunto stata quella di rilevare concretamente come un bambino percepiva ed organizzava i materiali presentati in uno schedario matematico differenziato.
Così abbiamo proposto in maniera disordinata il materiale che veniva fornito abitualmente agli allievi, chiedendo di ordinarlo …
La domanda era: la comprensione dei contenuti della matematica a partire da quali indizi si svilupperà? Quali criteri di analisi di pensiero andrà a proporre? Quali rappresentazioni svilupperà di tale disciplina? quali saranno le categorie (i raggruppamenti) che opererà?
Abbiamo visto che questi raggruppamenti corrispondevano solo parzialmente all’organizzazione logica del classificatore.
2.2 seconda indagine
La risposta a quella domanda porta ora ad una riflessione psico-pedagogica più larga.
E’ sufficiente dare un materiale affinché l’allievo riesca ad organizzarlo secondo criteri logici? affinché l’allievo ne abbia una cognizione ed una metacognizione arricchente?
E’ sufficiente presentare uno schedario affinché l’allievo comprenda la materia che esso raffigura, la materia che esso racchiude?
L’attenzione al materiale, più precisamente alla forma del materiale che viene offerto ai bambini, vale a dire il supporto, il medium grafico, cartaceo, ecc … in qualche maniera spinge l’allievo ad utilizzare tale materiale in maniera del tutto inaspettata, vedi sorprendente. Maniere appiattite sugli stimoli percettivi, legate ad una esecutività poco riflessiva, poco metacognitiva, modalità di fare percettivo-motorie, pre operatorie, o senso motorie da un lato, e a schematismi neuro comportamentali stile stimolo riposta dall’altro?
significanti e significato, figurale e operatorio
3 In poche parole, si dà per scontata l’organizzazione dell’apparato, dandone per scontati i contenuti presentati.
Figurativo ed operativo vengono così a confondersi in una nebulosa dai confini mal definiti …
3.1 Scontati … come se, data per scontata l’organizzazione di un determinato contenuto di conoscenza, l’allievo assuma automaticamente tale organizzazione della conoscenza in maniera cognitiva e metacognitiva. Vale a dire che l’allievo capisca, sappia agire e sappia dire perché la materia, ed i contenuti ad essa relativi, sono così organizzati … come se tali criteri di organizzazione corrispondessero all’immagine che l’allievo se ne fa in partenza, o ne ha, all’inizio della sua epigenesi.
O magari ci si illude che i contenuti saranno capiti ed acquisiti in seguito?
3.2 Scontati … come se i contenuti della materia siano oggettivamente e logicamente isomorfi all’organizzazione del materiale didattico.
Il che vale a dire: i contenuti di una materia sono il determinato materiale XY, concreto organizzato. La materia viene così a confondersi con il suo aspetto figurale. Come se la matematica fosse il classificatore di matematica. Come se la lingua italiana sia l’ortografia della stessa o i quaderni ortografici.
In termini epigenetici ed espistemologici, in fondo si tratta qui dello stesso errore che si attua regolarmente in aritmetica chiamando operazioni ciò che sono degli algoritmi. L’operazione della moltiplicazione scritta, ad esempio, non é che un algoritmo. Algoritmo che può essere insegnato, esercitato ed eseguito senza che il bambino abbia una reale comprensione del pensiero moltiplicativo e senza una nozione di reversibilità.
Sappiamo che la reversibilità di una azione ne definisce appunto il suo sviluppo in operazione.
Vediamo anche che un algoritmo di un calcolo, diciamo l’addizione scritta, può essere eseguito senza che il soggetto ne padroneggi concettualmente le proprietà distributiva, associativa, dissociativa, invariantiva.
E’ lo stesso errore per cui si confonde il materiale (composto da cifre, segni aritmetici, eccetera …) dalle operazioni che vengono fatte sul materiale, l’aspetto figurale confuso con quello operatorio (concreto o formale che sia). E’ lo stesso errore che porta a considerare il materiale, così come é disposto e così via, invece che considerare l’agire del soggetto che interviene con il materiale. Ciò che fa l’evoluzione cognitiva, ciò che é ragione d’essere del pensiero operatorio é l’osservazione dell’agire del soggetto …;
3.3 Ma in fondo la risposta é già nell’aria. Lì, da acchiappare quasi senza sforzo.
Se la matematica viene considerata isomorfa alla sua rappresentazione, qualsiasi sia la sua veste … ecco che rappresentazione e concetto vengono a confondersi.
Ecco che rappresentazione ed operazione vengono a confondersi.
Ecco che significante e significato vengono a confondersi.
In verità non esiste più distinzione fra significante e significato;
– il significante tende a divenire significato, specialmente per quei bambini che sono portati a ricercare sicurezza nelle ripetitività e nella meccanicità. Da un punto di vista epigenetico ci impantaniamo o ci apparentiamo ad una concezione della conoscenza di tipo figurale, simbolico, affettivo;
– in didattica il significante tende a diventare il significato anche per quei docenti che confondono e non distinguono i concetti d’azione, d’operazione, di rappresentazione, e i rapporti fra elementi figurali ed elementi operatori della cognizione.
3.4 E come chiedere se la finestra é la cornice di legno che la contiene o il panorama che ne traspare.
Un apparato differenziato è condannato a veicolare questa confusione fra significante e significato, fra elementi figurali ed elementi operatori della cognizione?
Come dice MacLuhan il medium é il messaggio.
Quale il messaggio degli apparati didattici – leggi schedari – della differenziazione?
Certamente ciò dipende dalla loro applicazione
3.5 Questa mancata distinzione può esser ascritta a insufficiente padronanza:
– della epistemologia dell’età evolutiva
– della psicologia dell’età evolutiva
– della pedagogia
– della didattica prese singolarmente o nelle loro varie relazioni.
4.1 Nella mia esperienza, vedo svariate maniere di considerare la pedagogia della differenziazione. Nel quotidiano concreto insegnamento, l’utilizzazione di apparati di differenziazione didattica, viene organizzata, fondamentalmente, attorno a degli schedari che prevedono un ricco ventaglio di esercizi, di variazioni degli esercizi e di progressione degli esercizi. I principi sono quelli della variazione degli esercizi, e della progressione per livelli.
4.2 A fronte di allievi che funzionano a ritmi e modalità personali, a fronte del riconoscimento di queste individualità, l’apprendimento differenziato (AD) viene oggi dato quasi per scontato.
L’AD non ha però valore di necessità, di nessun tipo. Non può essere considerato, e non deve venire considerato, necessariamente come l’esito naturale e/o logico del riconoscimento delle differenze individuali a scuola. L’AD è solo una, fra le molte, variazione del tema “come lavorare con allievi differenti”. Variazione sviluppatasi negli anni 60, a partire dalla psicologia comportamentista. Variazione non necessaria, ma solamente storicamente determinata. Tanto é vero che molta della psicologia evolutiva considera l’apprendimento cooperativo e argomentativo come due modalità assolutamente valide, altrettanto “logiche” e “naturali”, quale esito pedagogico didattico del riconoscimento delle differenze individuali nell’apprendimento. Non esiti inesorabili ma possibilmente scelte ponderate.
4.3 Le tendenze attuali sembrano portare ad un progressivo gonfiamento delle pratiche dette della differenziazione. Specialmente nell’applicazione di “pacchetti” pre-ordinati, quali classatori o schedari di percorsi multipli e a livelli.
In questo ambito, concetti come quelli di spazio prossimale di sviluppo trovano oggi una applicazione meccanica, diciamo pure di natura ed animo epistemologici, assolutamente de-personalizzata. Soggetti epistemici ma non epistemofilici, allievi che eseguono ma non allievi che dissertano …
Detto così, in verità, tutto ciò potrebbe non suonare, né bene, ne male. Io direi invece: perché affannarsi tanto, a che pro affidarsi a pesce ai materiali differenziati, ai classatori, agli schedari, eccetera, direi io se, e sottolineo bene il se, se non liberano la relazione?
4.4 Malauguratamente, il diffondersi di pratiche pedagogiche differenziate non va di pari passi con la riflessione e la formazione psicopedagogica del personale insegnante in generale. Molte volte, tutto passa poi senza una necessaria educazione al funzionamento eteronomo in un gruppo, né all’educazione gruppale. Stare in un gruppo, dispiegare algoritmi, dispiegare concentrazione e apprendimento individuale … Per molti allievi il gruppo esiste solo a ricreazione e/o nella strada. Attenzione: non considero il gruppo in sola accezione sociale, quanto cognitiva.
4.5 La memoria storica pedagogica é poi corta. Tali pratiche passano ai più come innovative, quando in verità erano già ampiamente diffuse e propagandate negli anno 60, a partire dalle applicazioni didattiche della psicologia comportamentista.
Salvo che negli anni 60 cominciavano ad andare di moda “i lavori di gruppo”.
4.6 Purtroppo i legami tra metodologie cooperative e metodologie individualizzanti sono purtroppo solo abbozzati dalla ricerca in pedagogia e in psicologia. Nella scuola, queste ricerche sono poco e male conosciute . Questa mancanza di riflessione porta ad applicazioni per lo più implicite di apparati pedagogici didattici di differenziazione con caratteristiche del tutto opinabili, ingiustificate e decontestualizzate.
Ma specialmente modalità di fare ed agire poco efficaci, magari proprio per gli obiettivi alla base dei principi della differenziazione.
In genere la generalizzazione degli apparati pedagogici differenziati si attua come razionalizzazione ed ottimizzazione delle risorse, come scelta o necessità, pedagogica, burocratico-amministrativa, in un contesto scolastico sociologicamente e clinicamente complesso.
Tutto ciò può comportare dei costi, può essere poco efficace, può degenerare a sviluppi tanto imprevisti quanto non voluti e non desiderati.
La lucidità e la consapevolezza permettono scelte esplicite. Lo sforzo di queste righe ha questo scopo.
5 Nella automatizzazione degli algoritmi, nell’eteronomo essere funzionale dell’allievo, la percezione del compito ne ha smarrito la cognizione, fattasi orami chimera impercettibile.
5.1 E’ allora poi possibile che, infine, gli approcci differenziati che basano la loro ragion d’essere sulla differenziazione del materiale possano ritrovare un legame diretto con la tradizione, tanto da, paradossalmente? rinnovarla, rinnovando la dipendenza, percorrendo meccanicamente l’apprendimento, chiudendo un sistema che si voleva aperto?
Si tratta di vedere, se – come, quando e perché, quale ne fosse la sua conclusione naturale – un materiale di differenziazione può portare un bambino ad una dipendenza dello stesso. In termini gestaltistici ad una dipendenza del campo.
6 Si tratta di considerare i rapporti fra cognizione, percezione ed organizzazione. In psicologia si considera ogni percezione come il frutto di una cognizione.
– Vale a dire: la percezione di uno stimolo é sempre diretta da una maniera specifica di considerare le cose.
– Per quanto concerne l’organizzazione il suo rapporto con la cognizione appare forse molto più chiaro e diretto. Consideriamo semplicemente che l’ordine é frutto dell’ordinare, quindi del raccogliere, del classificare, del differenziare, del mettere in relazione secondo determinati criteri, ecc. dei materiali che vanno messi in determinate posizioni.
7 In queste righe trattiamo di elementi cognitivi e di elementi procedurali un po’ contrapponendoli. Non è che siano veramente contrapposti. Ogni uomo cammina su due gambe. Ma se vanno di pari passo, vanno chiaramente distinti. Possono e vanno contrapposti. In verità sono implicitamente contrapposti in molte didattiche della rimozione del pensiero. Nelle nostre osservazioni abbiamo potuto interagire con ragazzi alternativamente impediti nell’uno o nell’altro registro (o ambedue). Così abbiamo ragazzi appiattiti sulle meccaniche e sulle procedure che non sanno pensare ed assimilare veramente i concetti, dove prevale un accomodamento senza assimilazione, una imitazione senza simbolo, un funzionare ossessivo, persecutorio. D’altra parte abbiamo bambini onnipotenti che assimilano senza accomodare, bambini che sviluppano conoscenze ma non procedure, o sequenze, o algoritmi automatizzati …
7.1 E’ altresì evidente che l’acquisizione di un algoritmo è necessaria per ulteriori sviluppi. Una buona padronanza degli algoritmi è necessaria per dare fluidità al pensiero, per non caricare la memoria con processi che vano automatizzati.
Ma una ossessiva e persecutoria esecuzione degli stessi non libera il pensiero. Anzi lo tiene occupato. Se non incatenato. Quanti sono i bambini che leggono ma non sanno cosa hanno letto. Quanti sono i bambini che sanno seguire le 4 operazioni ma “non amano” la matematica.
Per esempio: la lettura richiede un controllo sistematico della corrispondenza suono segno, vale a dire la decifrazione, specie quando si leggono parole difficili, nuove, o in un lingua straniera. Ciò deve essere fatto con pertinenza e rapidità.
Ma la lettura non è solo quello.
La lettura, intesa nel processo di comprensione di quanto letto, domanda il passaggio dal registro persecutorio (il controllo sistematico della corrispondenza suono segno) a quello rappresentativo, vale a dire il passaggio da un registro meccanico, o, al meglio, meccanizzato, di tipo percettivo motorio uditivo visivo a quello ideativo.
8 Insomma, qualsiasi schedario corre il rischio di porsi come strumento di confusione. Confusione fra significante (schedario) e significato (la materia). Fra forma e contenuto.
Fra elementi figurali ed elementi operatori della conoscenza.
Quarta parte
Sintesi
1 Questa osservazione mette in gioco vari osservabili:
– il linguaggio e il suo statuto nella relazione d’insegnamento apprendimento
– il ruolo del gruppo
– il ruolo della metacognizione
– la distinzione fra operazione e figurazione
– la distinzione fra ragionamento ed algoritmo
2 In termini generali la situazione proposta mette in luce l’abuso del concetto di autonomia.
Ab-uso = uso cattivo, irregolare, improprio, illecito. Fra autonomia ed eteronomia c’è una enorme distanza. La distanza fra la morte del pilota nell’aereo che precipita perché ha finito la benzina e la libertà di prendere un secondo aereo.
Ciò avviene quando tutto lo sforzo didattico del docente, o tutto lo sforzo d’apprendimento dell’allievo, o ambedue, mirano essenzialmente all’esecutività, al fare le schede, al compilarle, certamente al saper fare delle operazioni aritmetiche, senza considerare le proprietà delle operazioni, senza considerare l’organizzazione del materiale, senza proporre la lettura (= ipotizzazione e comprensione) dello stesso. In poche parole quando il materiale è dato come scontato e mirato unicamente ad un apprendimento algoritmico. La modifica dell’apparato, quando si modifica il materiale e il contesto di lavoro, vale a dire quando da uno schedario si passa ad un altro schedario o apparato didattico, – non è mistero – la modifica dell’apparato propone allora un passaggio traumatico, perché i soggetti si ritrovano inesorabilmente scoperti nella loro dipendenza di campo …
3 Questa dissertazione é relativa a una realizzazione concreta della differenziazione pedagogica. Non é relativa quindi alla sua impostazione generale e teorica.
Mi riferisco a una situazione concreta che ha messo in gioco una didattica della differenziazione, poco attenta ad esplicitare, differenziare, e quindi a coordinarli, gli aspetti algoritmici dagli aspetti cognitivi, quelli figurali, da quelli operatori.
Da un punto di vista epistemologico ed epigenetico assistiamo a vari salti fra campi di competenze e conoscenze differenti, che male dissimulano una mancanza di obiettivi e metodi costruiti all’uopo.
Abbiamo scoperto una didattica probabilmente tutta realizzata sul fare e poco o per niente sul saper dire. Una didattica tutta impostata sulla esecutività e poco sulla cognizione e la metacognizione; una didattica che opera una dissimulazione fra algoritmi (e apprendimento degli algoritmi) e ragionamento.
A fronte della cognizione questa è una frode.
Questione di mezzi e di fini.
Il mezzo si fa fine? Il mezzo si sostituisce al fine? per cui non si sa dove si va …
Bibliografia
Barth B.M, L’apprentissage de l’abstraction, Retz, Paris, 1987, Nouvelle édition augmentée 2001
Barth B.M, Le Savoir en Construction, Retz, Paris, 1993
Bateson G., Verso un’ecologia della mente, Adelphi, Milano, 1976
Bruner J., Il pensiero, strategie e categorie, Armando, Roma, 1973
Crahay M., L’école peut-elle être juste et efficace? De l’égalité des chances à l’égalité des acquis, Bruxelles, De Boeck, 2000
Gardner H., Formae mentis. Saggio sulla pluralità dell’intelligenza [1983], Feltrinelli, Milano, 1987
Gardner H., Educare al comprendere. Stereotipi infantili e apprendimento scolastico, Feltrinelli, Milano, 1993
Galli G., Il progetto di lavoro nella differenziazione matematica
Galli G., L’intelligenza senso-motoria a scuola. Senso motricità e pensiero a scuola, P & E, Psicologia & Educazione, rivista dell’Associazione Svizzera di Psicologia dell’Età Evolutiva, 2, 24, 1998, Solothurn
Galli G., Chi lo fa lo aspetti, meandri sullo sradicamento del pensiero, Brissago, 2003
Galli G., Sodi D., A che gioco giochiamo, Brissago 2006
Hirtt N., Avons-nous besoin de travailleurs compétents ou de citoyens critiques?, APED, mai 2001
Inhelder B., I disturbi dell’intelligenza, Franco Angeli 1985
Piaget J., Réussir et comprendre, PUF, Paris, 1974
Piaget J., La prise de consience, PUF, Paris, 1974
Piaget J., L’équilibration des structures cognitives, PUF, Paris, 1975
Vygotskij L.S., Pensiero e linguaggio, Laterza, Roma, 1990
Wittgenstein P., Ricerche filosofiche, Einaudi, Torino, 1967
Allegato A
Ecco la tabella introduttiva di Dimat, l’elenco, l’indice se vogliamo, di tutti gli argomenti che l’allievo deve conoscere. In seguito ci sono alcuni esempi di schede relative a vari argomenti
| Matematica classe 4a – tabella di autovalutazione | F | M | D |
| 1 Numeri 2 Segni aritmetici 3 Frazioni 4 Addizioni: calcolo orale 5 Addizioni: calcolo mentale 6 Addizioni: operazione scritta 7 Sottrazioni: calcolo orale 8 Sottrazioni: calcolo mentale 9 Sottrazioni: operazione scritta 10 Moltiplicazioni: calcolo orale 11 Moltiplicazioni: calcolo mentale 12 Moltiplicazioni: operazione scritta 13 Divisioni: calcolo orale 14 Divisioni: calcolo mentale 15 Divisioni: operazione scritta | |||
| 16 Misure di lunghezza 17 Misure di peso 18 Misure di capacità 19 Misure di valore 20 Misure di tempo | |||
| 21 Diagrammi |
Conoscenza dei numeri livelli F, M, D
Addizioni scritte livelli F, M, D
Moltiplicazioni scritte livello F, Misure lunghezza livello M
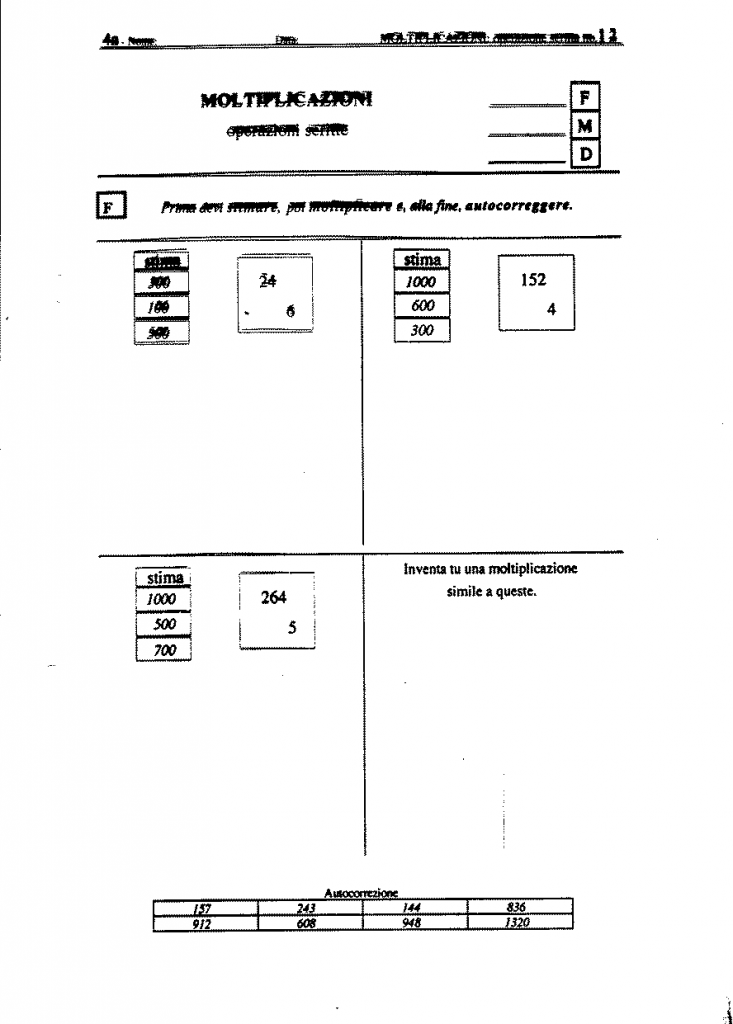

Allegato B
esempi di scheda originale
medesime schede senza indicazioni classificatorie