Chi lo fa lo aspetti, meandri sullo sradicamento del pensiero

Osservazioni, commenti, letture, punteggiature, relative alle difficoltà del saper ragionare a scuola

Avvertenza

A) Il titolo di questo testo: “chi lo fa lo aspetti” indica un proposito e un approccio metodico e metodologico del saper ragionare a scuola. E’ importante aggiungere quel “a scuola” al “saper ragionare”. Le situazioni che la scuola propone, le situazioni che implicano un ragionamento, sono ben specifiche, si riferiscono a contenuti definiti come ben vedremo poi in seguito.
La domanda fondatrice il titolo di questo testo é la seguente: “ma perché certi bambini (a scuola) non sanno ragionare?”

A quel titolo avrei voluto aggiungere un “primo”, messo lì a significare un prossimo “secondo”, testo futuro da scrivere? Quale la frontiera che li separa?
E’ una questione metodologica e una questione di contenuti.

1) Quella metodologica concerne l’approccio pedagogico didattico quotidiano relativo alle difficoltà di ragionamento a scuola (e non solo per chi si trova in età evolutiva …):
vuole dunque proporre uno sguardo e una lettura relativi a quelle difficoltà, vuole proporre concetti per permettere una comprensione delle ridondanze che sono il segno manifesto dello “sragionare” e per mettere in situazione di equilibrazione l’educatore e l’allievo.
Nei primi due capitoli di questo testo vedremo quindi di entrare in materia in questo esercizio: capire come mai i bambini non sanno ragionare a scuola, ma scoprire come mai noi stessi, quali educatori, ripetiamo gli stessi errori (magari imputandone tutte le cause agli allievi).

2) Questa questione metodologica é però anche di contenuto. Si tratta, vale a dire, di capire quali sono i contenuti che noi accordiamo al ragionare:
le modalità di lavoro del docente, piuttosto legate alle soluzioni da perseguire, alla ripetitività di pattern esecutivi, algoritmi aritmetici, ecc … piuttosto che mirate alle funzioni rappresentative e alle strutture della conoscenza, sono appunto dei contenuti che vogliamo affrontare.
Ma l’uso di una metodologia pedagogico didattica piuttosto legata alla domanda “cosa hai trovato” in contrapposizione a quella che chiederà “dimmi come hai fatto” o “dimmi come puoi fare” diventa appunto una questione di contenuti differenti da proporre a scuola.

B) Nella prima, e seconda lunghe parte di queste righe mi sono avventurato principalmente su un terreno abitudinario: quello che crede – per far ragionare il bambino, o per aiutare il bambino a sviluppare le sue abilità di ragionamento – che per ragionare non si debbano affrontare problemi reali ma piuttosto dei problemi aritmetici (oggi chiamate situazioni) o far leggere un testo …
Per portare i bambini sui binari del ragionare gli educatori potrebbero proporre molte altre cose. E si potrebbero intraprendere percorsi senza muoversi su quei simulacri di ragionamento quali sono i problemi aritmetici classici. Dovrebbero, potrebbero avventurarsi nell’ambito delle spiegazioni causali, che sia quello del mondo delle leggi fisiche, oppure della realtà delle relazioni fra persone …
Altri mondi e modi di operare potrebbero essere possibili … ma ciò lo sorvoleremo nella terza parte di questa dissertazione, sperando di poterla approfondire in un futuro molto prossimo?

C) Alla fine di questa lettura una domanda legittima potrà sorgere: perché non tuffarci immediatamente in terreni nuovi? ma allora perché una descrizione così lunga su quanto infine concerne solo una minima parte del saper ragionare?
Le risposte sono varie. Una la più semplice é la seguente: cominciamo ad approfondire quanto stiamo proponendo, prima di proporre qualcosa di completamente nuovo. Esplicitiamo quanto svolgiamo tradizionalmente, prima di avventurarci in qualcosa di ignoto. Fare chiarezza sulla “tradizione” serve a perfezionare la didattica quotidiana, serve a inscriverla in un approccio che sia evolutivo e creativo.
In secondo luogo prima di stravolgere tutto l’approccio didattico modificando approccio e contenuti cominciamo pure a modificare una sola delle due variabili. E’ quanto ho fatto considerando l’approccio, in quanto mi sembrava quello più potenzialmente ricco in sviluppi futuri. Inutile sarebbe proporre situazioni di esperienze fisiche, di relazioni causali solo per spingere gli allievi a clonare le medesime soluzioni … se così fosse limitiamoci a fare quello che già facciamo da sempre.
Insomma prima di tutto mi pareva importante capire cosa d’altro potevamo/dovevamo fare nel nostro modo di rapportarci al ragionare.
Infine una ultima spiegazione potrebbe riferirsi alle reazioni circolari secondarie e terziarie. In un certo senso è quanto viene proposto considerando di trattenere il più a lungo un oggetto (i problemi “tradizionali”) per variarne le modalità di interazione e percezione: esperienze per vedere, per rendere l’oggetto un oggetto permanente …

Per queste e altre ragioni solo nella terza parte giungo ad esplicitare quanto continuamente traspare:
ma sono i problemi aritmetici il terreno giusto par ragionare, sono i problemi aritmetici a favorire il ragionamento o viceversa il saper ragionare é un requisito per risolvere problemini aritmetici? Si impara a ragionare con i problemini aritmetici?
Nella terza parte di questo lavoro allora troveremo un nuovo inizio per nuove esperienze pedagogico didattiche.

Durante la stesura di questo lavoro ho avuto l’opportunità di partecipare a una serie di incontri in un gruppo di lavoro composto da: Ivano Crotta, Daniela Sodi, Silvia Righenzi, Augusta Binda, Sandra Stalder e Nerina Bonalumi, colleghi dell’équipe di Sostegno pedagogico, che ringrazio. Tra di noi abbiamo avuto modo di sperimentare quanto descritto.

parte prima

Come una ragnatela

1. Premessa

“L’abitudine é pericolosa. Per esempio bisogna essere prudenti con la prudenza, la prudenza divenuta abitudinaria é pericolosa. Un uomo che lava sempre le ciliegie prima di mangiarle, può facilmente una volta o l’altra bere l’acqua in cui le ha lavate e prendersi il colera, si dice”.

Bertold Brecht, Me-ti. Libro delle svolte, Einaudi 1970, pag. 99

“Ma questo bambino non sa ragionare, ripete sempre le stesse risposte, ripete sempre gli stessi schemi”. Quante volte abbiamo sentito un docente sconsolato ripetere questa frase? Quante volte nell’esperienza quotidiana dell’insegnamento e del sostegno ad allievi in difficoltà a scuola abbiamo vissuto e ripetuto la stessa esperienza?
Bambini che non ragionano …, in un mio articolo ¹⁾ – che rimane la base del lavoro presente – scrivevo:

Sovente … quando ci confrontiamo con un allievo che non riesce ad integrare gli insegnamenti in un insieme coerente, che non generalizza e non differenzia, che non scopre o costruisce regolarità, che non riesce a formulare ipotesi rispetto le proprie azioni, insomma di un bambino che ancora ragiona e si fissa sulle configurazioni, sovente, diciamo che questo bambino é ancora dominato da necessità percettive, ed eventualmente che si situa (ancora) ad un livello pre-operatorio.

Il pensiero più spontaneo e immediato, conseguente a quanto descritto, può essere quello di consigliare al docente, o al genitore, di insistere nella manipolazione di oggetti, affinché il bambino abbia ad esercitare sufficientemente le modalità a lui congeniali in quel momento … e ciò nella speranza che dette esperienze, queste ripetute azioni, lo portino automaticamente a delle operazioni.
Insomma siccome la resistenza si situa nell’incapacità ad abbandonare il dato sensibile e nel primato della percezione rispetto l’astrazione, come pure nell’azione con elementi figurali rispetto alle operazioni, ne prescriviamo la necessità e la continuità, sperando che una maggiore fissazione di queste modalità di “computazione” della realtà ne comportino automaticamente un loro superamento.

Quali sono le condizioni indispensabili in questo tipo di lavoro (quello consigliato ai docenti o ai genitori) affinché il bambino scopra le regolarità logiche, scopra (costruisca!) le conservazioni, costruisca e comprenda i valori posizionali nella costruzione del numero, sappia affrontare un testo con atteggiamento attivo di ricerca e scoperta, sappia fare delle inferenze, delle ipotesi, astrarre delle regolarità tra elementi percettivamente dissimili, ecc … ?

Cosa é che definisce le necessità percettive di un bambino? Quali sono le sue interne necessità che lo muovono in tal senso?

Allora, relativamente al soggetto, la prima domanda sarà piuttosto rivolta al suo esterno e ci porterà a riflettere sull’apparato psicopedagogico, pedagogico e didattico, a sapere come organizzare le esperienze, quali materiali proporre, che tipo di compito dare, affinché il bambino sia accompagnato nella scoperta e nella costruzione di strategie operatorie, ecc …; la seconda domanda ci porterà al suo interno, a riflettere sull’evoluzione psicologica del bambino.

Per riflettere sul funzionamento di questi bambini bisogna ben cominciare a riconoscere il pensiero senso-motorio, a identificarlo quando esso si manifesta a scuola e riflettere sul pensiero simbolico ed operatorio.

2. Mise en place

In questo testo prolungo dunque le riflessioni già avviate nel testo citato. E quello presente é comunque ancora uno studio di impronta epistemica, epistemofilica e clinica. Una ricerca senza pretese di esaustività, che viene ad aggiungersi al mio testo appena rammentato. Testo che, lo ripeto, sta a queste righe come le fondamenta a una costruzione.
Il presente testo é retto da due tracce di indagine:
– una epistemica, perché si basa sulla conoscenza delle tappe di sviluppo del pensiero del bambino;
– ed una clinica perché naviga con le difficoltà della cognizione, con i suoi arresti, con le sue accelerazioni e decelerazioni, con i suoi décalages, con le sue asimmetrie o sviluppi dis-uniformi.
Viaggeremo pertanto tra la pedagogia, la psicopedagogia, la psicologia scolastica, l’epistemologia, la psicologia dell’età evolutiva, la psicopatologia della cognizione e la filosofia dell’educazione.
In altri termini: tratteremo dunque di quella che può essere chiamata pulsione epistemofilica e delle sue disfunzioni.

Non ho realizzato una ricerca statistica, corredata di tutti i dati necessari sulla frequenza e la ricorsività di quanto andrò descrivendo (vedi poi gli esempi di “s-ragionamento” che riporto in seguito); non propongo nemmeno dati che possano inserire tali comportamenti in una tassonomia di competenze, o in apparato stadiale; come bello e importante sarebbe magari fare.
Ho descritto le osservazioni che ho potuto trarre dalla mia esperienza; ma ciò senza un apparato di ricerca e di osservazioni sistematizzate: siamo dunque ancora a un lavoro pilota, introduttivo, ritagliato nel tempo, e senza la dovuta continuità. Qua e là potranno dunque mancare dei nessi causali fra un paragrafo e l’altro …
Quelle che seguono sono osservazioni legate alla presenza e al manifestarsi di quello che ho già chiamato “il pensiero senso motorio a scuola” ²⁾. Comportamenti tipici e quotidiani; ma comportamenti indesiderati, non sempre sufficienti e pertinenti a risolvere i problemi proposti dal docente. Comportamenti che inesorabilmente, a scuola, si rivelano spesso essere una zavorra, come pure una zavorra alla scuola; patologie dell’apprendere, sclerotizzazioni o fossilizzazioni dell’apprendere.
Eccolo allora il pensiero che ha perso le sue radici, il pensiero che vede le sue origini sclerotizzate in quello che diventa talvolta un modo di funzionamento rigido, fisso, ripetitivo, senza possibilità di trovare vie di uscita?

Con i bambini di scuola elementare è lecito attendersi due tipi di funzionamento dell’apparato cognitivo, perlomeno con i bambini più piccoli. Vediamo un funzionamento di tipo senso-motorio, che si sviluppa nella prima infanzia, e uno simbolico, che si sviluppa a partire dall’avvento della funzione simbolica.
Queste due forme di conoscenza, di padronanza e di maniera di interagire con la realtà, sono mescolate tra loro e sono presenti sempre a scuola e nella vita. In forma e gradazioni fluttuanti. Traggono però la loro origine e il loro sviluppo in una età che dovrebbe essere precedente alla scolarizzazione. Questo in una situazione normale.
Lo stadio senso-motorio è stato ben descritto. Nella letteratura scientifica abbiamo una dovizia di osservazioni e spiegazioni.
Quanto io ho definito con tal nome si riferisce quindi a dei comportamenti che sono slegati dal ragionamento, dal saper comprendere, dal fare delle ipotesi e dal saperle controllare. Come difficile è vedere in questi comportamenti delle attività di anticipazione di un effetto (cioè di valutazione di un evento senza potere vederlo), ma sono piuttosto basati sulla percezione; sono comportamenti pure scarsamente argomentativi.
Essenzialmente percettivo e manipolatorio, il funzionamento senso motorio precede l’intuizione e il simbolo …
Ma quanto è descrittivo di uno stadio tipico e originario dello sviluppo del bambino… la stadio senso motorio appunto, viene dunque ripreso come concetto non più stadiale, ma di un modo di funzionamento. Un modo fra molti.
Sappiamo – ciò é ben descritto in molti modelli dello sviluppo del bambino – come la crescita dell’intelligenza non abbia un processo lineare. Ma questo si presenti con accelerazioni, regressioni, stasi. E poi sappiamo delle dissincronie, dei décalages, delle “viscosità”, ecc … Ci sono varie linee, vari livelli, diversi tipi di intelligenza e così via ³⁾.
In poche parole, sappiamo che l’apprendimento non è lineare e che accanto a sviluppi forti possono permanere atteggiamenti passati. I nuovi stadi, le nuove potenzialità e competenze non vengono a fagocitare totalmente quelle vecchie. Le passate disposizioni non scompaiono totalmente, ma rimangono, qua e là, a seconda degli interessi, delle motivazioni, delle esperienze del bambino, ecc …
Basti pensare alla lettura. Come questa possa essere oggetto di una trattazione intelligente oppure percettiva. Un caso è capire un testo e magari rispondere a delle domande o fare delle ipotesi. Un altro è saperne fare la dizione, saper far corrispondere il suono al segno. Se il primo è un processo che sgorga chiaramente dalle possibilità di inferenza del soggetto e può perfino necessitare di competenze formali per permettere al ragionamento il suo svilupparsi (come ad esempio la lettura di una tabella che riporti, quantificandone le probabilità, il numero di combinazioni possibili che un dato carattere genetico si manifesti dopo N generazioni), il secondo è un processo che rimane semplicemente ad un livello di ripetitività, una meccanica che nulla richiede alla comprensione, se non una iniziale costruzione della corrispondenza suono segno ⁴⁾.
Accanto ad atteggiamenti evoluti constatiamo la permanenza di altre competenze più primitive sul piano ontogenetico, ma ciò non di meno necessarie e importanti. Queste stesse abilità primitive sono necessarie nel ventaglio delle possibilità di risposta all’ambiente, alle sue variazioni e alle sue richieste. Possibilità multiple sempre attuali e attualizzate quotidianamente…

3. Desideri

Sono 4 le tappe necessarie per affrontare le difficoltà sorvolate, 4 i pantani pedagogici, le variabili e gli obiettivi del mio agire presente sul pensiero senso motorio. Almeno, quattro sono gli elementi che vorrei poter essere in grado di risolvere al fine di questo mio navigare:

riflettere quali sono i soggetti (bambini) che si scontrano su tali nodi. Farne una categoria, scoprirne e descriverne le caratteristiche generali. Finché li descriveremo solamente rispetto l’errore, l’attività o la scheda che li vede in scacco limiteremo le possibilità d’intervento, ne alieneremmo la fonte, costringendoci ad intervenire sempre e soltanto sulle risposte e non sulle dinamiche del bambino.
saper fare una lettura, ma una lettura che sia evolutiva. Sapere cioè inserire una data risposta in un percorso cognitivo, nell’evoluzione progressiva delle conoscenze epistemiche …
sapere e riuscire a capire perché un bambino si accanisce e si fissa su di una modalità. Quali sono i nodi, i blocchi che lo fissano su una data teoria, o su di una data modalità d’interazione con l’ambiente, su di una data modalità di risposta, senza essere in grado di cogliere e raggiungere modalità più evolute … ⁵⁾
trovare e sorvolare, se non proprio costruire, delle modalità di lavoro per affrontare almeno alcuni dei nodi e superarli …

Non possiamo limitarci ad una lettura caso per caso senza estrapolarne delle regole. Saremmo condannati alla creazione perpetua di schede da proporre all’allievo, senza avere la certezza che le competenze esercitate vengano generalizzate, e ciò senza restare inchiodate a contesti decisamente specifici o iper specializzati.
Perbacco, non che ciò sia disdicevole, tutt’altro. La creazione di manuali d’uso e di curricoli d’apprendimento di nozioni e competenze di contenuto sono sicuramente auspicabili ma escono dalle competenze e dalle possibilità presenti. Così come escono dalle intenzioni del sottoscritto. Ciò che importa maggiormente é trovare delle costanti e delle regole sulle quali intervenire. Costanti e variabili possibili, che permettano di farci capire e di farci agire in maniera creativa e generativa: modelli generalizzabili e differenziabili ogni qual volta ci troviamo impantananti nelle difficoltà del ragionare. Modelli e variabili che ci diano qualche pista di indagine e di lavoro creativo.

Lavoreremo sulle modalità allora, piuttosto che sui prodotti. Sulla modalità di accesso ad una informazione o sulle modalità di computazione della stessa, sui processi di costruzione delle conoscenze piuttosto che sulle conoscenze stesse. Un po’ come entrare in un periodo operatorio (secondo il modello piagetiano) dovremo staccarci dalle configurazioni per osservare noi stessi, ciò che facciamo, ciò che agiamo ⁶⁾.
Ma agiremo pure con noi stessi proprio come potremmo proporre agli allievi …

parte seconda

Costanti e variabili

4. Costanti e variabili: costanti

Regolari sono le situazioni che viviamo a scuola, frequenti, ripetute, conosciute: come l’insuccesso scolastico degli allievi e come l’insuccesso del nostro agire. Regolari e ricorsive, le difficoltà si manifestano frequentemente. Sono una costante del nostro lavoro. Vediamone degli esempi.

A) Esempi

Nota: tali esempi sono tratti quasi tutti dalla mia esperienza quotidiana, alcuni mi sono stati riferiti.

Questi esempi si riferiscono a molte bimbe e bimbi di:
– età e classe differenti,
– ambedue i sessi,
– provenienze geografiche e culturali disparate,
– varia estrazione socio culturale.
Siccome non stiamo effettuando uno studio stadiale ma riflettendo sul modo di funzionamento ho volutamente omesso di indicare l’età, come pure classe e sesso dei soggetti. Non é appunto importante conoscere questi dati perché non sono pertinenti alle osservazioni svelate. Questi, in effetti, sono comportamenti giustificabili oppure no, consoni alle aspettative oppure no, relativamente all’evoluzione (età) del soggetto. Evidentemente dipendono molto dall’età del bimbo e dalle sue esperienze.
Domanda: a quale età possiamo aspettarci di rilevare un determinato comportamento?
Siamo di fronte a una domanda falsa perché tutti i comportamenti rilevati sono e non sono contemporaneamente attendibili. Corrispondono a una tappa nell’evoluzione delle conoscenze del soggetto, corrispondono a un saper fare e a un saper dire dell’allievo, corrispondono alle sue spontanee teorie, alla sua evoluzione, alla sua comprensione dell’oggetto, alle sue possibilità di risposta. Sono segno di un funzionamento per copioni ⁷⁾, di schemi rigidi, dove il ragionamento non interviene a modificare procedure già fossilizzate. Sono il segno di una tappa evolutiva.
Questa la domanda da fare ogni volta, e indipendentemente dall’età del soggetto: quale era la teoria sottostante, quali sono state le variabili, le ipotesi agite e controllate dal bimbo. Cosa l’ha spinto a rispondere a tal modo?

Esempi senza commento

Gli esempi seguenti sono descrizioni quanto più brevi possibile e fedeli a quanto osservato nella mia pratica psicopedagogica.

1. conservazioni e trasformazioni (contando soldi)
XY prende una banconota da 20.- Fr. e una moneta da 20 ct. La somma é 40.

2. il doppio (cantando una canzone)
Un coro di 10 bambini canta una canzone in due minuti. Quanto impiega a cantare la canzone un coro di 20 bambini?
Risposta: 4 minuti perché é il doppio

3. valore posizionale
XY esegue il calcolo seguente:
508 + 34 =
Dice: “tolgo l’8 rimane 50”

4. valore posizionale
Con il materiale Cuisnaire XY dice che:

= 32 oppure = 23

Queste risposte sono date indifferentemente (cioè senza tener conto dell’orientamento spaziale dei legnetti).
In seguito oriento i legnetti proponendo contemporaneamente tre configurazioni. Allora si ottiene:

= 32

= 23

= 2

5. nominare
XY mi chiede:

– Quando facciamo la lettura?, indicandomi il classificatore che abbiamo sul tavolo. Le chiedo quale lettura. Lei ripete:
– Quando facciamo quella lettura?.
– Quale? chiedo io.
– E XY con il dito mi fa cenno al classificatore:
– Quella lettura.
E io ripeto:
– Quale lettura?, senza permetterle di cercarla per mostramela.
Il giochetto va in avanti due o tre volte ancora. Infine XY mi dice:
– La lettura della passeggiata.
Cioè infine nomina il testo.

6. memorizzazione del calcolo
XY sa eseguire mentalmente e a memoria i calcoli seguenti:3 + 2
5 + 4
6 + 3
8 + 1
2 + 2

invece quelli seguenti li deve calcolare sulle dita
13 + 2
15 + 4
16 + 3
18 + 1
12 + 2

7. sciando
Su di un campo di sci XY vuole deve fare una gara di slalom. E’ la prima volta. Gli spiegano che deve passare in mezzo alle porte. Ebbene XY passa letteralmente in mezzo alle porte, piegando le ginocchia e passando sotto alla stoffa ogni volta.

8. tecnica del calcolo, algoritmi
XY, classe 3 (9;3) esegue la sottrazione seguente:855 –
178 =

Alle unità esegue:
“5 meno 8 non si può, allora faccio 15 meno 8.”
Conta sulla dite e trova 7.

Poi ripete sulle decine:
“C’é il riporto. Allora 5 meno 8 non si può, allora faccio 15 meno 8”
e conta di nuovo immediatamente sulle dita.
Gli dico “ma non l’hai appena fatto?”

Il bimbo mi guarda di sottecchi e dice: “… quanto faceva … (passano 7 o 8 secondi ) … ah già sette”.

9. la divisione
XY deve dividere un gruppo di 15 musicassette in tre parti.
“Ah, é come fare a pezzi una torta”
E sul disegno frantuma le cassette in tre.

10. percezione dei numeri – valore posizionale
Mostro con le mani delle quantità, indicandole con le dita. Ciò velocemente al fine di favorire la ritenzione mnemonica.
Sposto le mani vicino XY, a destra, sopra la testa, ecc … modificandone la posizione nello spazio.

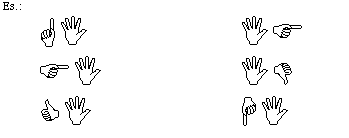
Ebbene se un momento le dita erano 6, cambiandone la presentazione davanti XY queste possono diventare allora 5 e 1, oppure 1 e 5, cosa che é ancor giusta seppur indice della difficoltà; ma possono pure diventare 51, oppure 15.

11. a tavola
Un bambino apparecchia la tavola alla scuola dell’infanzia. Mette piatti e posate. Il menù prevede una minestra.
Un compagno gli dice di cambiare “perché la minestra si mangia con la fondina” (non con il cucchiaio). Il bambino non capisce più cosa deve fare.

12. conversando
Dopo un parto di un fratellino a scuola si parla delle nascite, delle mamme partorienti, del “mettere alla luce i bambini”. Si propone un disegno dei Ebe appena nati come momento per la discussione. Ebbene non pochi disegnano i bimbi sotto dei lampadari e affermano di non sapere perché vengono messi sotto una fonte luminosa.

13. orientamento
I bimbi usano fogli di classificatore per un esercizio. Sono abituati a prenderli e metterli sul tavolo con “i buchi dalla parte delle finestre” , affinché siano per inserirli poi correttamente nel classificatore.
Ecco basta che il bimbo sia orientato di 180 gradi, seduto al contrario, o in un altra aula che, mettendo i buchi dalla parte delle finestre, utilizzi il foglio in maniera scorretta per il suo inserimento nel classificatore …

14. contrari
Grande – piccolo,
nero – bianco,
giorno – notte,
leggero – pesante.
… chilometro?
…ortemolihc!

15. conoscenza del numero
Filippo, in classe quinta, guarda una sottrazione in colonna:

767 –
764=

A lato do un foglio con i numeri seguenti

3 – 72 – 628 – 1314

E chiedo “senza calcolare, prova a indovinare rapidamente quale può essere il risultato?” Da annotare che lascio guardare la sottrazione per un solo istante, poi la maschero.
Risponde 628 perché “ha tre cifre”.

Stessi esempi a 4 cifre

3624 –
3623 =

4000-
3999 =

con le proposte seguenti

1 – 10 – 100 – 1000

16. conoscenza de numero
Un docente sta presentando un sistema di rappresentazione del raggruppamento per decina di un insieme numerico. Ciò per introdurre il valore posizionale relativo alla base 10.

Racconta alla classe: “ecco ogni 10 palline facciamo un sacchetto …”. Una bambina non ha capito, o ha poco ascoltato (il che equivale alla stessa cosa). In seguito il docente dice: “bene adesso fate l’esercizio. Fate come me”. Ebbene la bambina riproduce esattamente lo stesso raggruppamento eseguito dal docente (due sacchetti e poi ancora tre palline, che equivale a 23), anche se il numero degli elementi o degli oggetti non corrisponde alla situazione stimolo (per esempio aveva 45 palline), non applica dunque il raggruppamento in base 10 alle differenti situazioni proposte. E ad ogni nuova situazione, ad ogni nuovo insieme numerico, non capisce perché non riesce ad eseguire rapidamente il raggruppamento “due sacchetti e poi ancora tre palline”., non capendo cosa deve fare con tutte quelle palline che avanzano.

Esegue una azione, non una operazione.

17. dizione
La lettura, silenziosa o non, quando é unicamente manifestazione della corrispondenza tra segno scritto e suono. Cosa che non é altro che una corrispondenza termine a termine e che converrebbe forse semplicemente chiamare “dizione”.
A scuola si confonde ancora spesso e volentieri il comprendere un testo e la sua dizione.

18. numeri con l’accento
I numeri con l’apostrofo e i numeri con l’accento. L’attività proposta si prefiggeva di trattare e di valutare diverse schede equivalenti ma con una progressiva estensione numerica:

(esempi delle schede)

	Conosci bene i numeri entro il 1000?
La cifra 3	quanto vale nel numero 638?	………………..
	e nel numero 103?	………………..
La cifra 7	quanto vale nel numero 754?	………………..
	e nel numero 972?	………………..

	Conosci bene i numeri entro il 10000?
La cifra 2	quanto vale nel numero 4623?	………………..
	e nel numero 4276?	………………..
La cifra 5	quanto vale nel numero 4053?	………………..
	e nel numero 5904?	………………..
	e nel numero 2245?	………………..

	Conosci bene i numeri entro il 100000?
La cifra 2	quanto vale nel numero 92003?	………………..
	e nel numero 28976?	………………..
	e nel numero 5,2?	………………..
La cifra 5	quanto vale nel numero 5803?	………………..
	e nel numero 98154?	………………..
	e nel numero 1821?	………………..
	e nel numero 12,58?	………………..

Ebbene Adelmo non sa (più?) distinguere ciò che é numerico da ciò che é linguistico, la virgola dei numeri decimali dalla virgola del testo. Tutto diventa confuso e indistintamente apostrofo o accento. Ciò che é identico é il segno grafico.

19. linguaggio prescrittivo
Una collega incontra un bambino alla scuola dell’infanzia. Fanno una attività e le dice: “guarda sul quel tavolo c’é una matita, prendila”. Il bambino guarda e si dilunga un po’ con tutti gli oggetti che sono sparsi sul tavolo. Forse non ha nemmeno bene capito quanto deve fare o forse ha visto qualcosa di più interessante. La collega spazientita da questa perdita di tempo allora dice: “eh cerca di muoverti un po’”. Il bambino allora si mette a saltellare ed agitarsi e poi dice: “ma guarda, non ho mica capito perché mi hai detto di muovermi”.

20. pittura …
Un collega deve rispondere improvvisamente al telefono durante una seduta di lavoro quando stava realizzando una figura sagomata, un personaggio. Prima di staccare la cornetta il collega rapidamente dice: “pittura il vestito”, il bambino esegue prontamente l’invito pitturando il proprio vestito, cioè quello che indossava.

Esempi con commento

21. tecnica del calcolo, algoritmi

648,35-
227,14 =

23347,12-
21188,67 =

XY quando dice che: “i due calcoli sono differenti perché il secondo è più lungo”, dimostra di aver ben imparato la didattica ufficiale che imposta la difficoltà crescente dei calcoli relativamente alla quantità di cifre che essi riportano (sig!).
Non vede i riporti, non s’avvede della necessità di effettuare dei riporti e del numero di riporti da gestire, e poi non ha minimamente bisogno di padroneggiare il valore posizionale e tanto meno i decimali. Basta sapere incolonnare, come una disposizione spaziale, una “buona forma”.

22. letture percettive (di problemi)

1) Ho comperato 8 bastoni di pane da 2 Kg. Quanti Kg. Di pane ho comperato in tutto?8 + 2 = 10

In tutto compero 10 bastoni di pane.

2) Il papà ha fato rifornimento di benzina diverse volte. Il mese scorso per due volte ha preso 36 litri. E per altre due volte 24 litri. Quanti litri ha preso in tutto?

36 +24 = 60

In tutto ha ricevuto 60 litri di benzina

3) Il papà muratore va a lavorare. La sua ditta sta costruendo 2 case in due posti differenti. Va 2 volte al primo posto (il lunedì e il martedì). E’ distante 36 Km. Nell’altro posto va 3 volte (mercoledì, giovedì, venerdì). E’ distante 24 Km. Il papà quanti Km ha percorso in tutto per andare a lavorare?

2 +2 + 36 + 3 + 24 = 67

Il papà fa 67 Km.

4) Gioco a bilie. Alla fine della partita me ne rimangono 10. Quante ne avevo all’inizio se ne ho perse 4?

10 – 4 = 6, ho perso 6 bilie

commento
E’ evidente che il tipo di lettura di questi problemi è percettiva. XY Riporta in ordine la prima cifra scritta, poi la seconda e così via. L’ordine percettivo corrisponde all’ordine aritmetico. Nel quarto esempio l’ordine descrittivo poi non corrisponde a quello cronologico reale, perché il gioco comincerebbe con: “Ho 14 bilie …”
In oltre XY trascrive qualsiasi numero scritto in cifre …

23. imboccare
Un bambino ripete, per imitazione, l’atto d’imboccare. Imbocca una bambola, ripete l’atto, muove il braccio. Ma per lui tutta l’attività, a questo stadio, si risolve nell’aspetto motorio, muovere il braccio meccanicamente e ripetutamente. E’ questo un esercizio funzionale, della funzione che muove il braccio … é una reazione circolare.

commento
Un’azione simbolica si manifesta quando, ripercorrendo la stessa situazione precedente il bambino si immagina i risultati della sua azione, il nutrimento del Ebe, i suoi capricci, ecc…
Per esempio quando muove le labbra nel gesto di mangiare … Abbiamo qui un passaggio dal semplice fare meccanico a un fare simbolico. Da un gioco funzionale, meccanico-esecutivo (magari di tipo imitatorio) a un gioco simbolico.

24. sottrarre
Su una scheda di calcolo c’é scritto “esegui la sottrazione seguente”. Ebbene il bambino non sa cosa fare. Solo quando sentendo un suo compagno o sbirciando s’accorge che da qualche parte c’é tracciato il segno “- ” (meno>) dice “ah devo fare il meno”.

commento
Il segno grafico meno ha fatto scattare un pattern di tipo esecutivo, immediato e meccanico. Ma il bimbo non é giunto al simbolo (la lingua é un sistema di simboli), tanto é vero che non sa fare il collegamento tra esso e il termine “sottrazione” che rimane incompreso, pure dopo vari anni di frequenza scolastica.

25. permanenza dell’oggetto
Con Franca faccio un gioco, un gioco progressivo, o una progressione di giochi. Qualcosa tra il gioco di Kim e il Memory.
Prendo delle figurine e comincio con il gioco di Kim (nel gioco di Kim si tratta di costruire una fila o una serie di 4, 5, 6 oggetti (o figurine) e poi chiedere al bambino di ricostituire la sequenza dopo averla manomessa). Franca deve memorizzare le postazioni relative ad ogni immagine che io metto in fila davanti al lei. Uso 6 o 7 figurine. Quando ha ben memorizzato le postazioni io cambio il posto di alcune figurine. In progressione poi ne aggiungo magari delle nuove che non c’entrano, o ne tolgo.
Ebbene Franca rapidamente e correttamente ricostruisce la sequenza iniziale, eliminando le eventuali nuove figurine o ricuperando quelle tolte.
Ha dunque ben memorizzato non solo tutte le figurine, ma anche le rispettive posizioni nella fila.
In un secondo momento faccio la stessa cosa con 6 o 7 parole scritte. Stessi sviluppi.

Da notare che il materiale é stato scelto appositamente con Franca al fine di eliminare oggetti sconosciuti e parole sconosciute. Il vocabolario é controllato e tutto legato all’esperienza di Franca.

A questo punto riprendo le figurine, che capovolgo (quindi non si vedono più, situazione tipo Memory) rispettando però la stessa disposizione sequenziale precedente.
Ebbene se chiedo a Franca di dirmi in quale postazione si trova una carta che io nomino (“dove sta il sacco” , ” dove sta il la pesca”, ” dove sta il treno” …), prontamente me la indica senza errori. Quando io le chiedo di nominarmi la carta indicandogli una postazione (“cosa c’é qui”?) non me la sa nominare. Con le parole scritte si ripete esattamente la stessa dinamica. Quando le do il nome mi mostra il posto, quando indico il posto non mi sa più dare il nome. Questo succede diverse volte anche modificando il materiale.

commento
Franca sa trovare dunque una figura o una parola nascosta se le dico il nome. Se le indico la postazione e chiedo di denominare la carta non é più in grado di farlo. Non sa cioè risalire alla denominazione di un oggetto o alla sua raffigurazione simbolica scritta quando non ha un indizio percettivo per farlo. Sa cosa è una pesca, sa cosa è un treno e così via, sa ritrovarli in una posizione nascosta come quella del memory ma non è più in grado di giocare a partire dalla sola posizione.
Per riuscire ha bisogno di un imput nominale (il nome: “pesca”, “treno” ecc …) oppure visivo, scritto (le grafie relative ai vari oggetti).

E’ un problema di permanenza dell’oggetto. Ai primi stadi senso motori descritti da Piaget il bimbo non sa ritrovare un oggetto nascosto sotto uno straccio … La permanenza é parziale; é possibile o attuata solo a partire da una percezione dell’oggetto, che scatena poi uno schema attivo … La permanenza é parziale perché necessità di un dato percettivo (in questo caso anche nominale) che facilita il compito. Un indizio necessario per scatenare il ricordo di quanto già percepito. Una percezione parziale, come il biberon semi mascherato che il neonato riconosce per quello che é, ma che non sa riconoscere se il mascheramento é troppo grande. Un problema di gestalt si potrebbe pure dire, di buona forma … di una forma che si manifesta in presenza di sufficienti elementi …

26. stereognosie
Un bambino sa rispondere in situazione di stereognosia tridimensionale (3D) di un oggetto – “ho in mano una mela”. Ma non é in grado di rispondere in situazione di stereognosia bidimensionale (2D).

commento
La mela, non é il disegno della mela, la scala non é la sua raffigurazione, l’uovo non corrisponde al suo profilo di forma più o meno ovale …
Forse l’esperienza stereognosica 2 D é difficile perché manca una immagine più direttamente correlata con l’oggetto fisico … la stereognosia 2D di un oggetto (per esempio il profilo cartonato di una mela) equivale alla stereognosia della sua immagine (vale a dire alla stereognosia di una costruzione di una rappresentazione).

27. classificazioni
Con Adelmo, all’inizio dell’anno scolastico, riordino il materiale di matematica (DIMAT). Questo é organizzato in maniera tale che il programma é suddiviso in un numero preciso di argomenti, nel programma in questione sono 21, con una progressione facile, medio, difficile. Così il bambino, davanti a lui si ritrova 63 fogli – corrispondenti a 63 “test” – relativi agli argomenti e ai tre livelli di difficoltà. Ogni foglio ha la sua intestazione e numerazione relativa all’argomento. Il bambino riceve tutto il materiale già ordinato.
Da notare che sono già due anni Adelmo lavora con questo sistema e il materiale appena ricevuto é identico a quello dell’anno precedente.
Ebbene io elimino tutti i riferimenti “classificatori”: le intestazioni (titolazioni dei 21 argomenti) presenti su ogni foglio, le numerazioni (in quanto la titolazione ha una sua numerazione associata). Lascio solo le consegne relative alle operazioni aritmetiche, le misure, i numeri, ecc … su ogni foglio tolgo dunque ciò che serve per ordinare il materiale nel classificatore, e lascio tutto quanto é relativo all’esecuzione di operazioni aritmetiche. Lascio pure le indicazioni facile, medio, difficile.
Eliminati i riferimenti descritti, mescolo i 63 fogli é chiedo al bambino di ordinare il materiale secondo i suoi criteri.
Da notare che i raggruppamenti spontanei non corrispondono per niente a quelli del materiale. Adelmo raggruppa per esempio schede che concernono operazioni aritmetiche di segno differente, oppure di misure differenti, ecc …
Ecco alcune sue verbalizzazioni:

“vanno assieme perché hanno … i cerchi” (nei fogli presi ci sono dei numeri sparsi inscritti in una forma circolare);
“vanno assieme perché hanno … la mano” (qui c’é una mano come elemento iconografico per indicare qualche cosa);
“vanno assieme perché hanno … i quadrati (stessa cosa come per i cerchi);
“vanno assieme perché hanno … c’é scritto indica e indicare” (nel testo della consegna Adelmo scopre queste parole);
“vanno assieme perché hanno … queste colonne”;
ecc …

commento
In questo caso quale allora la funzione del linguaggio? Quella di raggruppamento e descrizione logica? Oppure di descrizione di pattern?

28. automobiline
Tito, un bimbo di cinque anni e mezzo, gioca con i suoi compagni. O forse sarebbe meglio dire che imita il gioco dei compagni ma sempre agendo un po’ in ritardo rispetto a loro. Giocano con il materiale Lego.
Per esempio un compagno prende una automobilina e la fa viaggiare su una stradina. Poi fa sembiante che sale in montagna. Con la voce fa il rumore del motore.
Tito guarda imbambolato, poi, con un certo ritardo, rispetto il compagno fa la stessa cosa, praticamente esattamente la stessa cosa, ripetendo reiteratamente la serie di movimenti (ha guardato e memorizzato bene la scenetta) – intanto il compagno ha continuato la sua storia facendo viaggiare ancora l’automobilina, facendo intervenire dei personaggi ecc …
Intanto Tito funziona ancora a livello ripetitivo: fa i rumori della automobile, muove il braccio in alto e in basso (cosa che continua a fare per un minuto), ma senza costrutto simbolico. Per lui il gioco consiste nel fare brum brum e muovere il braccio, il gioco stesso é dire brum brum e muovere il braccio.
Non sa cosa fare d’altro, non ha nessun slancio creativo, il brum brum e il muovere il braccio non sono legati a una storia ma fini a sé stessi.

commento
Tito non sta giocando simbolicamente, non sta agendo una storiella come il compagno, ma sta giocando con il corpo e la voce, fa “azioni per ripetere” (reazioni circolari). Questo tentativo di entrata in relazione di Tito con il compagno fallisce perché questi non trova in Tito un interlocutore sul piano simbolico. Ma poi che tipo di tentativo é?
E’ interessante anche rilevare come tutto questo per Tito avviene senza parole e suoni, tranne la onomatopea del motore. Il gruppetto dei compagni, invece descrivono ciò che fanno, fanno proposte, fanno parlare i personaggi, variano le onomatopee …
Dopo questa scenetta Tito ne imita un’altra, sembrerebbe quasi che sta per entrare nel gioco, ma finisce col ripetere la stessa dinamica descritta con l’automobilina.

29. schemi …
A una bambina di terza elementare ho proposto una schema di raccolta di informazioni e dati che riguardava storielle e racconti vari più o meno fittizi.
Dopo la lettura del testo la bambina era invitata a rispondere a delle domande. Una serie di domande sempre uguale per ogni testo differente. Sulla scheda, accanto a ogni domanda, avevo poi tracciato delle righe, ciò a indicare lo spazio dove scrivere le risposte.
Qualcosa di questo genere:

Domanda 1	…………………………………………………………………………..
Domanda 2	…………………………………………………………………………..
Domanda 3	…………………………………………………………………………..
ecc..	…………………………………………………………………………..

Questo tipo di esercizio, mirato a un atteggiamento di ricerca attiva di indizi in un testo, e che speravo potesse essere appreso e generalizzato, é stato esercitato per una decina di volte, sino a quando un giorno consegno un nuovo esercizio con lo stesso schema tranne che per l’indicazione delle righe in cui scrivere. La variazione che avevo proposto era dunque formata da un aspetto di occupazione del foglio, non avevo più indicato dove il bimbo avrebbe dovuto scrivere le sue risposte.
Non l’avessi mai fatto. La bambina entra in crisi: “ah ma questo non lo so fare, non so rispondere a queste domande, no no é troppo difficile”.

Ebbene cosa é successo? La bambina invece di porre delle domande che provvisoriamente adesso vorrei chiamare “domande cognitive” ha fatto delle “domande percettive”. Invece di dire/chiedere: “non c’é lo spazio per scrivere, dove devo scrivere, posso avere un foglio per scrivere le risposte che qui non posso”, ecc … s’é bloccata di fronte la constatazione non espressa: “qui le righe non ci sono”. Invece di fare una lettura legata alla comprensione del testo, ha fatto una lettura legata alla percezione dello spazio grafico del compito …

commento
Se la domanda formulata é percettiva, cioè legata alla disposizione sullo spazio del testo scritto é perché il pattern esecutivo ha avuto il sopravvento rispetto la comprensione del testo, oppure perché lo schema del pattern esecutivo viene a fissarsi comunque su basi percettive ancora troppo pregnanti. Sarebbe bastata una piccola ricognizione del tipo: ma questo testo ha sempre le stesse domande. In verità la bimba non ha prestato attenzione al tipo di domande ma alla loro disposizione.

Un medesimo dispositivo di risposta, almeno quello che io ritenevo fosse un dispositivo identico, si avvera fuorviante per la bambina.
Sicuramente lei si é limitata ad osservare la disposizione spaziale, per così dire, dello schema di domande e spazi dove scrivere, non certamente il tipo di domanda. Se io pensavo di potere generalizzare lo schema di domande la bambina ha solamente, per ora generalizzato la disposizione spaziale. Per questo e non per altro s’é bloccata di fronte al compito e solamente con un mio intervento regolatore é riuscita ad ammettere ed accorgersi che tutto era identico: certamente, sul piano cognitivo, non sul piano percettivo.

30. relazioni
Chiedo a XY (in classe prima) di seriare una storiella di quattro immagini. Precedentemente ho provato anche farle seriare storielle di sole tre immagini. Purtroppo per il momento XY riesce a funzionare solo a coppie – e ancora temporalmente non coerenti come vediamo nelle due accoppiate seguenti – , vale a dire che propone una serie successiva di coppie senza costrutto logico temporale. In questo caso XY ha proposto le seguenti accoppiate dopo una lungo riflessione.

Primo accoppiamento

Secondo accoppiamento

Qui XY commenta la terza immagine: “la mamma sgrida la bambina”.

commenti
Immediatamente vediamo come per XY saper raccontare quanto succede é difficile. La difficoltà linguistica é apparente nei termini che usa: “disco”, “aprire” (invece che rompere” … Non sa spiega perché, bloccata nell’argomentare ulteriormente la scena.
Ecco l’estremo realismo, l’attaccamento stretto all’immagine, che non é una palla. XY non riesce a nominarla. Inconsapevolmente ne definisce la forma geometrica. Come R. Magritte che, di fronte al suo quadro della pipa che fuma, afferma: “ceci n’est pas un pipe”. Certamente perché il disegno della pipa non é la pipa.
Nessuna esigenza di coerenza temporale viene a mettere in crisi le risposte i XY. La sola crisi che può vivere é quella del docente che la mette in una situazione per lei ingestibile …
Allora vediamo che:

come detto non c’é relazione temporale,
c’é una lettura diretta, dell’immagine senza definire un prima e un dopo. Non c’é cioè storia ma sola lettura delle immagini. Le immagini non sono sequenze di una storia …
non c’é relazione fra i personaggi:- la bambina prende
– la mamma sgrida
probabilmente tale storiella mette in gioco la paura delle punizioni di XY e le punizioni che magari ha subito nel passato
non c’é passaggio all’esperienza. XY non ha esperienze, almeno non c’é relazione tra disegno, elementi del disegno e realtà fisico-sociale (il rotondo).

La lettura é diretta, realistica. XY probabilmente ha problemi nella relazione con l’altro. Non agisce le relazioni, sia temporalmente nelle sequenze inverse, sia con i personaggi. Ciò che descrive é separato, alienato dalla relazione con gli altri.

31. nominare
XY sta controllando una scheda di calcoli. Le chiedo “quale stai controllando?” Lei risponde: “questo”, indicandolo col dito. Io dico: “si ma quale”? “Questo”. In seguito mi allontano di qualche metro per scrivere un altro calcolo sulla lavagna. Le chiedo quindi: “adesso quale calcolo stai controllando”? Io ho una copia della scheda in mano. XY dice ancora “questo”.

commento
Non sa dire se sta controllando il primo, il secondo, il terzo, … l’ultimo calcolo.
Il vocabolario è limitato all’indicazione spazio percettiva.

B) Scuola

“Il matematico Ta disegnò davanti ai suoi scolari una figura molto irregolare e pose loro il problema di calcolare la superficie. Essi suddivisero la figura in triangoli, quadrati e circoli e altre figure geometriche di cui si può calcolare la superficie, ma nessuno riuscì ad indicare proprio esattamente l’area di quella figura irregolare. Allora il maestro Ta prese delle forbici, ritagliò la figura, la mise sul piatto di una bilancia, la pesò e mise sull’altro piatto un rettangolo facilmente calcolabile, da cui tagliò via dei pezzi, finché i due piatti si trovarono in equilibrio. Me-ti lo chiamò un dialettico, perché a differenza dei suoi scolari, che confrontavano soltanto delle figure tra loro, egli aveva trattato la figura da calcolare come un pezzo di carta avente un peso (risolvendo cioè il problema come un vero problema, senza curarsi delle regole)”

– Bertold Brecht, Me-Ti. Libro delle svolte, Einaudi 1970, pag. 53

Sovente si sente dire di questi bambini: “non sanno ragionare”.
Ebbene allora qual’è lo statuto del ragionamento, qual’è lo spazio che comunque nella scuola si accorda al ragionare?
Quante volte mascheriamo le nostre stesse incomprensioni e la nostra ansia di fronte al bambino che non ci dà la risposta che noi vogliamo?
Troppe volte poi crediamo di dare delle situazioni che favoriscono il ragionamento, quando invece purtroppo non ci avvediamo che non facciamo che riproporre ricorsivamente situazioni simulate dove la risposta c’è già, solamente il bambino non la conosce ancora. In verità quante volte non chiediamo ai bambini di risolvere un problema, ma gli chiediamo di riprodurre uno script, di darci la risposta che noi vogliamo?
“La banalizzazione diviene una panacea pericolosa quando l’uomo l’applica a se stesso (…) Al momento in cui lo studente fa il suo ingresso nel sistema scolastico, egli é una imprevedibile “macchina non-banale”. Non sappiamo quale risposta darà a una certa domanda. Se però alla fine ottiene i risultati che il sistema si aspetta da lui, le risposte che darà alle nostre domande dovranno essere note in anticipo (…) I testi scolastici sono un mezzo per misurare il grado di banalizzazione. Se lo studente ottiene il punteggio massimo, ciò é segno di una perfetta banalizzazione (…) Non sarebbe affascinante immaginare un sistema d’istruzione che chieda agli studenti di rispondere solo a “domande legittime”, cioè a domande le cui risposte siano ignote” ⁸⁾?

Quante volte poi l’ansia del bambino, ma pure la nostra, quella del docente, hanno il sopravvento e lo spinge, ci spinge, a dare sempre e comunque la solita soluzione, in mancanza di altre possibilità?
Se la coazione a ripetere ha il sopravvento questa ha un significato. Vuol dire che la percezione del compito, la percezione che il bambino ha del compito, ma come pure la percezione che noi abbiamo degli insuccessi del bambino, sono entrate in un circolo vizioso. La percezione del compito induce alla ripetizione di copioni precedentemente codificati, di copioni che in precedenza sono state oggetto di un processo di insegnamento/apprendimento che aveva ricevuto dei feedback in qualche modo positivi. Dei feedback che spingono il soggetto a perseverare con un tipo di risposta assurto a copione, a un modello che si può ripetere.
In verità si tratterebbe di operare un salto di gestalt. Si tratta di valutare le azioni in gioco, si tratta di capire e vedere: ma come valuto io?
Il problema dell’apprendimento è un problema di insegnamento. Il problema dell’allievo è il problema del docente: di-segnare, in-segnare … ⁹⁾
Quello della sragionare è l’immagine della ripetitività, dell’applicazione indeterminata di una modalità, di una soluzione a tutte le situazioni che sembrano uguali. E’ pure l’immagine di una impossibilità: quella di raggiungere nuovi superiori traguardi.
Ma allora di cosa parliamo e di chi parliamo? Dell’allievo o di noi?
Appare evidente allora che la stessa scuola, senza avvedersene, chiama i bambini a funzionare in modo senso motorio. Ci mancherebbe che non lo faccia! Lo scrivere deve diventare un processo automatico, ripetitivo, senza pensiero nella sua veste ortografica. Il calcolare ugualmente: un calcolo scritto, una divisione, una addizione devono essere effettuate senza intoppi, il loro algoritmo deve funzionare senza pensieri.
Una immagine: un uomo seduto alla tastiera. Video, processore, hardware, ecc … l’apparato meccanico, fisico, realizza i calcoli aritmetici, le dita schiacciano i tasti, al video appaiono segni grafici, immagini, ecc … addirittura faccio fare una correzione ortografica automatica. Si scrive “l’uomo infila l’ago” oppure “l’uomo infila lago”. Il computer è fermo. L’uomo pensa. Scorporiamo dunque la parte tecnica da quella riflessa.
Gli apprendimenti meccanici saranno certamente una parte del compito dell’insegnante. Compiti legati agli automatismi, non legati all’intelligenza.
Le macchine possono calcolare. Di conseguenza il calcolo è la forma più bassa d’intelligenza. Tutto ciò che si deve imparare meccanicamente è pregiudizio, non è conoscenza.
La conoscenza comporta degli aspetti soggettivi, dei significati personali, oltre che un significato esterno.

La difficoltà dell’insegnamento semmai sta nel distinguere. Nel separare le necessità ripetitive (immaginate una tennista come Serena Williams o Martina Hingins senza automatismi) dalle necessità riflessive, creative.
Distinguere: per meglio capire come realizzare progetti che possano portare il bambino ad imparare e imparare ad imparare; distinguere: per avviare progetti che lo portino a staccarsi dal dato percepito.
La difficoltà sta poi quando queste necessità di ripetitività vengono a generalizzarsi in maniera non appropriata.
E’ quanto sono andato osservando a scuola con i modi di fare e di trattare la realtà, con i modi di apprendere, o con i modi di concepire l’apprendimento che possono essere descritti o definiti come senso motori o percettivi, o percettivo-senso-motorio ¹⁰⁾.
Vale a dire modi dove il soggetto agisce sulla ripetitività, sulla percezione delle configurazioni, sul copiare delle immagini o delle azioni nella maniera più fedele (realistica) possibile. Constateremo allora come delle Gestalt quasi archetipiche, dei modi di fare vengano assunti a modelli difficilmente intercambiabili; “buone forme” (si fa per dire) poco generative … ¹¹⁾
Eppure quante volte possiamo dire di essere di fronte ad una attività veramente generativa?
Intanto sappiamo che l’eccesso di prescrittività del curricolo e degli insegnamenti possono portare a risultati fallimentari dell’apprendimento. Infine la costante, immediata, regolare e puntuale
valutazione degli apprendimenti, specie se fatta agli inizi, porta i bambini alla paura e influisce su di loro spingendoli a muoversi in modo non creativo.

La domanda a sapere quanto la scuola deve lavorare sul prodotto e quanto sui processi è di fondamentale importanza. La scuola si presta per sua natura ad insegnare (trasmettere) tutta una serie di risposte e comportamenti a variazioni ambientali sotto controllo. Tutto il programma consiste in una successione di variazioni controllate dei dati da presentare agli scolari. Il programma scolastico si presenta come una sistematica di obiettivi e proposte, una didattica tesa ad ottenere e fornire delle risposte, piuttosto che teso alla creazione di divergenze e alla formulazione di domande aperte.
Le proposte fatte dai docenti hanno già le risposte. E tali risposte sono necessarie per il normale svolgersi del programma. Il programma, senza le risposte attese, non può certamente svolgersi. Quelle risposte sono importanti affinché il programma non venga ad arenarsi su scogli imprevisti … Questo almeno lo svolgimento auspicato, che non è certo esente da scottature possibili, ed anche auspicabile almeno per una parte.
Certamente che il programma scolastico deve fondare sulle risposte il suo modo di essere: lo scolaro deve ben dimostrare di saper rispondere alle esigenze normative della scuola, ma deve sempre farlo anche nel suo modo di agire?
Ma la focalizzazione sulle risposte necessarie , vale a dire l’eccessivo peso dato all’apprendimento di script fissi per situazioni statiche e controllate è forse la causa principale che porta sovente le difficoltà a lavorare sui processi ¹²⁾.

Quante volte possiamo dire che la scuola lavora sui processi mentali quali:

la conoscenza, con la capacità di archiviare e di rievocare il materiale memorizzato,
la comprensione, capacità di afferrare il senso di una informazione,
la generalizzazione, impiego di dati conosciuti a nuove situazioni,
l’analisi, separazione degli elementi costitutivi alfine di evidenziarne i legami,
la sintesi, riunione di elementi al fine di creare nuove strutture coerenti,

oppure sul ascolto o sulla fissazione di immagini interiori ¹³⁾, ma ciò in maniera specifica?
La scuola ha una visione essenzialmente o elettivamente cumulativa del processo di apprendimento, e forse talvolta solo quantitativa. Lavora sulle conoscenze, ma con le conoscenze quali contenuti da trasmettere e accumulare. Propone programmi di complessità crescente (nel senso che si costruisce su di una successione di insegnamenti che diventano dei pre requisiti per quelli successivi, come per esempio nelle competenze di calcolo, o di scrittura). Un apporto qualitativo teso ai processi e alle strutture del pensiero sembra mostrarsi adesso nei suoi valori più che complementari …

Vediamo quindi come spesso l’insegnamento sia una azione di tipo “imperativa”, vale a dire che dice all’allievo come deve svolgere una determinata cosa …
Von Foerster dice anche che sovente confondiamo segnale ed informazione. L’informazione, afferma, non sta nell’oggetto (che sia un libro, una video) ma nel azione (computazione) che il soggetto fa su di loro. L’informazione deriva dalle operazioni che il soggetto svolge sull’oggetto.
Spesso succede allora che un bambino in difficoltà, il bambino che non sa ragionare, si comporti come una “macchina comportamentismi”. Dove, questo bambino in difficoltà, funziona correttamente solamente con un linguaggio imperativo, cioè dove l’informazione é uguale al segnale ¹⁴⁾. In fondo si propone costantemente un paradigma di tipo neo comportamentista. Si tratta di “abbandonare quella strategia che ci spinge a cercare tra gli oggetti al di fuori di noi per adottarne un’altra che ci permetta di andare alla ricerca di processi dentro di noi ¹⁵⁾.

C) Differenziazione?

livello dell’intelligenza e strutture dell’intelligenza

A scuola tutti sono concordi. Un allievo viene descritto come molto intelligente l’altro meno, un terzo é svogliato e il quarto non capisce niente, un quinto é debile. Tutti sono quotidianamente concordi nell’utilizzare queste etichette, e apparentemente sono in situazione di doverle utilizzare regolarmente. Ma queste non sono categorie psicopedagogiche che descrivono oggettivamente l’allievo, sono piuttosto l’espressione di una soggettiva e implicita idea che la riuscita scolastica sia correlata con un livello d’intelligenza. Possono pure essere segno di una difficoltà del docente a cogliere le difficoltà evolutive di un allievo. Difficoltà che viene inconsciamente rimossa o mascherata da una azione di etichettatura dell’allievo. Etichettatura che solleva il compito del docente di trovare soluzioni in quanto dando una spiegazione para scientifica di quella risma, reifica una origine interna al bambino, una irreversibilità, una impossibilità alla modifica, “non ci si può fare niente, ho già provato io” (con un lapsus avrei scrittoetichettadura, perché quando l’etichetta c’é, marca poi duramente e lungamente il curricolo dell’allievo).
Ma ecco che quando si deve definire l’intelligenza questa concordia scompare.

Purtroppo la conoscenza (infarinatura) dello sviluppo del bambino, la conoscenza del suo sviluppo epistemico (come la conoscenza dello sviluppo affettivo, libidico e sessuale), non riesce sempre e automaticamente a portare la scuola e la pedagogia reale a una reale comprensione e applicazione concreta di quanto la psicologia dello sviluppo ha potuto produrre come comprensione degli stadi, delle funzioni, delle dinamiche e così via dicendo.
Non é facile riuscire a capire e situare un errore di ragionamento (di un bambino o di un adulto) all’interno di un percorso evolutivo. Un percorso che ha i suoi décalages, le sue spinte, le sue accelerazioni, le sue resistenze, le sue motivazioni, i suoi blocchi, le sue ansie e così via …

Per capire le difficoltà di ragionamento di un bambino, fra altre cose bisogna sapere ben distinguere quello che é il livello d’intelligenza da quelle che sono le strutture dell’intelligenza. Almeno, questo può essere il primo passo sulla strada della comprensione delle difficoltà di un allievo. Il secondo, ma non per ordine di importanza e nemmeno cronologico, essendo poi quello della valutazione affettiva, della motivazione, dell’ansia, dei fantasmi, ecc …
Livello d’intelligenza e strutture dell’intelligenza non sono assolutamente la stessa cosa e non sono automaticamente correlate. In verità possiamo avere differenti problematiche legate alle competenze e alle strutture dell’intelligenza.
Fondamentalmente possiamo avere 4 tipi di profili:

++	+-
-+	—

Ognuno di questi “profili” corrisponde a una tipologia che andrebbe ben compresa e definita ¹⁶⁾.
In verità se la scuola crede (talvolta) di intervenire sulle strutture del ragionamento, in realtà invece interviene sempre e volentieri sui contenuti.

Ebbene, detto questo, sappiamo anche che oggi nella scuola non si tratta più di perorare la causa delle differenziazione dei programmi. L’idea di percorsi d’apprendimento personalizzati é ben accetta. Ciò che non é in chiaro e come si deve differenziare e cosa si deve differenziare ¹⁷⁾.
In prima approssimazione possiamo considerare che se l’idea di differenziare si sviluppa, questa non tocca i programmi o le modalità di azione dell’allievo, non tocca le sue strutture della conoscenza. Affronta solo i programmi senza modificarli ma permettendo all’allievo un suo incedere personale. Ciò che si differenzia é la velocità, il ritmo di acquisizione …
E questo é un primo importante passo. Ma a condizione di non fermarsi li. Appare appunto evidente che tale prassi é di per sé insufficiente; e ciò quando non si avvede che qua é la, sparsa sul suo sentiero, incontra delle resistenze … Non vorrei che tutta l’idea della differenziazione si banalizzi nella antidemocratica, fatalista dimissione. Lasciare un allievo al suo punto d’arrivo ¹⁸⁾ … lasciare un allievo marciare al suo ritmo senza far nulla per modificarne il livello di motivazione e di aspirazione. Senza affrontare le sue intrinseche difficoltà.

Da un lato, se si accettano i bambini disadattati, se si attua una tolleranza rispetto le loro difficoltà sviluppando un programma differenziato, succede che queste stesse difficoltà vengano annullate ad ogni salto di classe. Vale a dire la promozione a una classe successiva non comporta una continuità nel percorso dell’allievo che si ritrova a dover attuare degli apprendimenti che cominciano senza tener conto del suo percorso precedente.

D’altro lato accettando questa prassi di dare dei materiali differenziati (più facili, o di livello inferiore) ci si muove sempre e preferibilmente sulle conoscenze, mai sulle strutture, o sui “contenitori”.
E’ un problema grosso grosso questo qua. Che fare con un bimbo che non sa ragionare? Basta modificare l’entità delle cifre di un problema aritmetico (invece che 500, 50, oppure 5)?
Sarebbe un po’ come svilire tutto quanto un soggetto deve saper mettere in atto per risolvere un problema.

Esempi:

cosa pensare della moltiplicazione quando il soggetto é fisso ad un pensiero additivo?
cosa pensare della misura della lunghezza e delle trasformazioni fra misure equivalenti, se il soggetto é fisso a una modalità di conservazione della marca non ancora operatoria?
cosa pensare del ragionamento logico di un qualsiasi problema aritmetico quando il soggetto non é ancora capace a sviluppare una inclusione di classi?
o cosa pensare della lettura di una storia poliziesca se il bambino non é capace a farsi uno scenario della stessa. Cioè non sa decodificare il testo in immagini, perché non conserva il senso di quel testo?

Allora dovrebbe apparire in qualche modo l’idea che si deve ben intervenire sulle strutture, che se un bambino presenta difficoltà di ragionamento non basta dargli materiali più facili, non basta differenziare e non fare nulla d’altro …

5. Costanti e variabili: variabili

Variabili invece sono le risposte, gli elementi di lettura e le ipotesi che potremmo sviluppare di fronte ad un insuccesso. Variabili perché in un contesto pratico, concreto dovranno riferirsi alla particolarità di ogni situazione. Variabili che si possono applicare ad ogni singolo esempio descritto in precedenza. Di volta in volta le situazioni descritte precedentemente potrebbero essere messe in luce con un concetto piuttosto che un altro.

a) Bersagli

“Me-ti disse: Ogni maestro deve imparare a smettere di insegnare, quando ne é giunto il momento. E’ questa un’arte difficile. Pochissimi sono in grado di farsi sostituire, a tempo debito, dalla realtà. Pochissimi sanno quando hanno finito di insegnare. Certo é duro stare a vedere come lo scolaro, dopo che si é tentato di risparmiargli gli errori che abbiamo commesso noi stessi, ormai fa proprio quegli errori. Se é brutto non ricevere consigli, altrettanto brutto può essere non avere il diritto di darne”.

– Bertold Brecht, Me-ti. Libro delle svolte, Einaudi 1979, pag. 66

Il bersaglio di queste righe è dunque duplice e ambivalente la riflessione sullo sragionare a scuola. Chi stiamo osservando, a chi rivolgiamo le nostre attenzioni, quali sono i soggetti del nostro riflettere?

Evidente appare la doppia valenza di queste osservazioni sulle difficoltà del ragionare e sull’errore, come pure le riflessioni ad esse rapportate.
Stiamo parlando dell’allievo che non sa ragionare, che ripete meccanicamente sempre le stesse vecchie soluzioni a contesti nuovi … certamente siamo partiti da li. Ma pure possiamo considerare che l’oggetto del nostro riflettere non siano i bambini, ma il docente stesso, noi stessi, quando dobbiamo modificare la nostra lettura di una situazione e modificare le risposte che abbiamo generalizzato arbitrariamente, forzando soluzioni che non fanno altro che perpetuare la nostra ansia di fronte l’allievo che non riesce; come perpetuano pure lo scacco delle nostre soluzioni.
Quando le soluzioni stesse diventano il problema ¹⁹⁾ … Chi lo fa lo aspetti, questo il titolo di questa riflessione, certamente perché chi fa un errore può certamente aspettarsene un altro.

b) Tappe

Come mai un bambino non ragiona? Partiamo da questa domanda. Ci sono allora almeno tre facce, tre aspetti da investire, tre tappe da effettuare quando ci si trova di fronte un errore.
La prima cosa da fare sarà di individuare il tipo di pensiero che regge la risposta a un dato problema e farne la lettura; saperlo fare e sapere inserire il comportamento in un quadro di coerenza interna (al soggetto). E’ questo un problema epistemologico. Si accompagnano con esso un problema metodologico ed uno affettivo.

Attenzione però alla natura dell’errore. Non trattiamo dell’errore di computazione. Trattiamo degli errori di ragionamento.

Errore di computazione
Es.:
30 + 20 = 40
gato con una “t

Errore di ragionamento
Es.: gioco a bilie con Carlo.
Carlo ne vince 7
ed io ne avevo 12.
Alla fine quante bilie mi rimangono?
7 + 12 = 19

Gli errori di computazione si distinguono nella loro natura da quelli di ragionamento. Si basano sul controllo ripetitivo di tecniche e competenze che vengono applicate nei ragionamenti.

1) A) un problema epistemologico

Si tratta dunque di leggere l’errore del bambino, capire come mai lui ha prodotto proprio quel tipo di risposta, perché ha proprio eseguito un compito in quella data maniera (ricordo comunque ancora che non stiamo pensando adesso a degli errori di tipo computazionale (tipo 8 + 3 = 12, oppure di un errore ortografico, competenze queste che si riferiscono a competenze meccaniche, ripetitive e non a delle capacità di ragionamento).
Se il bambino da una data risposta é perché tale risposta sottostà a un suo preciso schema, corrisponde a una sua precisa idea (più o meno spontanea, o appresa), si riferisce a un modello che ritiene corretto, ed é il modello che lui possiede che lo porta a tale “errata” conclusione”. E’ espressione di un dato livello, o di uno stadio specifico nell’acquisizione delle strutture di pensiero relative a quel campo scientifico. La conclusione del soggetto, la riposta che formula nei confronti del “problema”, si basa proprio su quel modello interiorizzato e non può essere altro senza modificare il modello stesso. L’elaborazione di una altra risposta implica la elaborazione di un altro modello. L’elaborazione di un altro modello implica la ri-elaborazione della situazione problema.
Saper leggere dunque, saper fare una lettura delle risposte del bambino, questo il primo passo da svolgere. Ma saper fare una lettura evolutiva, una lettura che sappia inserire quel dato comportamento in un quadro di riferimento esplicito; che sappia cioè inserire un dato risultato in un modello di riferimento evolutivo ed anche epistemico.

Non si può continuamente rinviare l’incontro con le teorie del soggetto. E’ vero che la scuola deve pur portare lo scolaro alla scoperta delle soluzioni che esse vuole, che deve portare lo scolaro a ripercorrere il programma. Ma non si può ignorare quanto di soggettivo (e comunque di attivo ²⁰⁾) lo scolaro propone continuamente … La scuola (ma pure il genitore e l’allievo che sono però inconsapevoli) in verità continua a definire “errore” ciò che in verità dovrebbe essere definito come “idea primitiva”, oppure “concetto di base”, ecc … una teoria o rappresentazione del soggetto, una teoria più o meno spontanea, una teoria forse ingenua, ma che risponde a una concezione che il bambino è andato sviluppando spontaneamente o in classe.
Non tenere conto delle teorie spontanee e delle modalità di ragionamento dell’allievo comporta uno scollamento, magari crescente, tra teoria insegnata e possibilità del soggetto a generalizzarla.

Sapere, capire perché un bambino si accanisce, si fissa su di una modalità, quali sono i nodi; scoprirne la “vischiosità”²¹⁾, un blocco, che sia percettivo o rappresentativo, una difficoltà legata alla permanenza dell’oggetto, una immaturità epistemica … (Come meravigliarsi, ad esempio, di fronte le difficoltà in geometria – quella insegnata alle scuole elementari é notoriamente euclidea – con un bambino fisso a uno stadio topologico? ). Ecco quanto fare in questa prima tappa. Ma sapere, capire perché un bambino si accanisce, si fissa su di una modalità, ci porta pure ai blocchi affettivi.

1)B) ma pure epistemofilico

L’intelligenza quale manifestazione di rappresentazioni, investita di passioni, invischiata in catene associative, sottomessa alla compulsione di ripetizione e al principio di piacere, é notoriamente collegata all’universo inconscio, dove si lega e si slega ai movimenti pulsionali e ai giochi del fantasma. I meccanismi di identificazione, di identificazione proiettiva, di transfert e di contro-transfert dominano alla grande ogni tentativo di crescita e di autonomia … La spinta epistemica, l’origine epigenetica dove traggono linfa se non dallo spazio transizionale che l’allievo crea tra sé e il mondo, tra sé e il docente …

2) un problema metodologico

Si tratta di operare una modifica radicale nel sistema di trattazione dei dati. Da una modalità percettiva, di riproduzione, potremmo pure dire di copia, dei risultati (come possono essere quelle del calcolo aritmetico o dell’ortografia) si tratta di passare a una modalità che tenga conto dei processi.
Ciò significa tre cose:
la prima è che non devo più solamente guardare le soluzioni (percezione diretta dei dati presentati). L’osservazione di ciò che io faccio va al di là di quanto sto ottenendo ma deve proprio portare su quello che sto facendo. In questo senso, se osservo la modalità, non mi posso più basare solamente sui dati sensibili (come poteva essere la soluzione erronea, fissata nero su bianco).
E’ questo il secondo significato: che dalla percezione passo all’evocazione, in quanto le operazioni svolte dal soggetto – in quanto eseguite – escono dal dato percettibile ma rientrano in quello dell’evocazione
Terzo significato. Ricordate le conservazioni? Che si tratti della sostanza, dei liquidi, del peso, della quantità numerica, ecc … il bambino dà una risposta operatoria quando riesce a staccarsi dal dato percettivo (i livelli d’acqua differenti, l’apparente maggiore numerosità di perline allargate, ecc …) e sa dire, per esempio, “non é cambiato niente perché non ho tolto nulla e non ho aggiunto nulla”. Per il bambino questo é certamente una questione epistemico. Il bambino dà quella risposta perché il suo livello lo porta a ciò. Ma quanto è epistemico per il bambino (deve diventarlo anche per il docente, come visto nel punto precedente) deve diventare metodologico per il docente.
Il problema per il docente é metodologico. L’esempio delle conservazioni ci deve far riflettere sulle domande che poniamo ai bambini. Queste vertono sulle soluzioni: “dimmi cosa hai trovato”; oppure vertono sui processi: “dimmi come hai fatto”, o “dimmi cosa hai fatto”. Questo é un salto molto grande perché troppo sovente siamo basati sulla soluzione.
… anzi probabilmente l’indagare sulle modalità potrà pure a illuminarci sulle teorie (l’epistemologia) del bambino.
La concezione dell’insegnamento, la concezione reale, quella praticata quotidianamente, é una concezione delle relazioni allievo-docente basate sulla ripetizione e l’imitazione delle soluzioni e degli script. Di convergenza delle rappresentazioni spontanee verso modelli sovente impliciti, di scarsa sperimentazione e di povero confronto argomentato …

3) un problema affettivo

Un ragionamento costa. Costa energie e costa ansia: nella gestione dello stesso, nell’attesa della risoluzione, nell’attesa della risposta del docente, nella paura della sua reazione …
Si tratta di gestire l’ansia che un ragionamento può costare per un bambino. Cosa dire di una situazione come quella che vediamo nelle figure riportate dall’esempio numero 30. Di fronte a una attività di argomentazione di quella storiella non esistono soluzioni preconfezionate, non c’é il solito modo d’uso. Si tratta di elaborare delle ipotesi verosimili, di raccontare una storia, un piccolo avvenimento che nulla ha a che fare con le soluzioni giuste o sbagliate.
Il dare sempre e solitamente la stessa risposta (vedi ad esempio un problema aritmetico) risponde a una necessità; quella dell’abbassamento dell’ansia che ogni situazione “problematica” comporta.
Ripeto cioè qualcosa che (sbrigativamente e in apparenza) mi rassicura, che non mi pone problemi che mi toglie la paura di non saper rispondere, che toglie la paura della reazione del docente (quando sbaglio), che mi sbarazza rapidamente dalla tensione legata al ragionare …
La natura dell’errore é sempre valutata nella sua dimensione cognitiva e troppo poco in quella affettiva.
Questa dimensione è fondamentale, specie perché quella apparente sicurezza che manifesta l’allievo quando ripete sempre le stesse soluzioni rischia di diventare una coazione a ripetere di stampo masochista (del tipo: ripeto comunque ciò che si avvera regolarmente sbagliato). Entriamo quindi in un mondo di forti insicurezze.
Il costo che comporta il ripetere qualcosa che si rivela regolarmente sbagliato deve essere sicuramente molto alto. In verità per l’allievo si avvera molto più costoso gestire la reazione dell’adulto. E’ molto più difficile gestire l’errore che la riuscita. E’ molto più difficile gestire le reazioni dell’altro suscitate dal mio (magari ripetuto) errore che quelle suscitate dalla mia riuscita. E’ pure molto più difficile gestire le emozioni e le reazioni che sgorgano dal mio inconscio … Queste sono le situazioni tipiche che infiammano il contro- transfert aggressivo del docente che si sente messo in gioco, si sente colpito narcisisticamente dalle ferite inferte dall’allievo “stupido” …
L’onere principale dell’errore non è la sua trattazione meccanica, epistemica, è la sua trattazione dinamico- affettiva.
Bisognerà lavorare sull’errore, la sua natura, la sua gestione e la legittimità che ha in un contesto evolutivo e che deve avere in un contesto di apprendimento come quello della scuola.

Parole chiave

“Si sa con quale profitto le nazioni scrivano la propria storia. Lo stesso profitto lo trae anche l’individuo singolo che scriva la propria storia. Me-ti diceva: Che ognuno diventi il suo proprio storiografo, allora vivrà con maggior cura e maggiori esigenze”.

-Bertold Brecht, Me-ti. Libro delle svolte, Einaudi 1979, pag. 106

cLa mente umana possiede una capacità organizzatrice che permette al soggetto di interagire con l’ambiente. L’apprendimento non è correlato unicamente alla maggiore o minore esposizione agli stimoli esterni, ma pure allo stadio evolutivo del soggetto. Alcuni concetti possono aiutarci a condurre le riflessioni epistemiche e psicopedagogiche.

linguaggio
In una vecchia ricerca ²²⁾ era stato riscontrato una forte correlazione tra deficit verbale e deficit figurativo. E’ frequente osservare che i bambini che “non sanno ragionare”. Possiedono pure poche competenze argomentative. Il linguaggio, per loro, tende ad avere piuttosto una funzione descrittiva della qualità fisiche degli oggetti e della realtà, una funzione di fotocopia della realtà. Usato in una veste che direi realistica, dove a dominare non sono le funzioni comunicative, quanto piuttosto quelle prescrittive ed imperative. Il linguaggio serve cioè ad impartire ordini, a descrivere un oggetto o degli algoritmi, ecc …

Secondo Vygotskij il pensiero non è altro che una interiorizzazione dell’interazione sociale. La qualità delle relazioni gioca un fattore determinante. Su questa linea Bruner afferma che è importante aiutare il bambino a nominare (vedi per esempio l’esempio numero 5, oppure n° 32) ciò che trova nell’ambiente e ad orientarsi nel tempo. L’insegnamento risulta facilitato dal linguaggio verbale che non è soltanto un mezzo per lo scambio, ma è lo stesso strumento che il soggetto utilizza per organizzare la realtà. Imparare parole, fare frasi corrette, non significa solo usare in modo corretto, il vocabolario, l’ortografia, la sintassi, ecc …, significa principalmente imparare ad organizzare la realtà.

memoria
E importante distinguere due aspetti della memoria di:
1. ricognizione o riconoscimento: consapevolezza che un oggetto percepito è già conosciuto, che fa parte della propria esperienza. Gli indizi di riconoscimento sono generalmente quelli che fanno parte della percezione. Con la permanenza dell’oggetto solo una parte dell’oggetto può portare al suo ricordo.
2. evocazione: rappresentazione mentale di un oggetto o evento con la consapevolezza di richiamare una esperienza precedente. In situazione può evocare, anticipare un effetto in base alla memoria legata all’esperienza. L’evocazione si fa in totale assenza dell’oggetto o dell’esperienza.

tentoni (attività per tentativi ed errori) Tatonnement
Le attività per tentativi ed errori sono attività di sperimentazione, di ricerca. Si distinguono tra quelli:
non sistematici,
non diretti o semi diretti,
fortuiti, dove la scoperta della soluzione avviene per caso.
Si parla di attività per tentativi ed errori sistematiche o dirette quando queste ultime sono illuminate dagli schemi precedenti che conferiscono dei significati alle scoperte fatte, quando c’è un legame causale tra azione e d effetto.

permanenza dell’oggetto
La permanenza dell’oggetto è la nozione del possibile ritorno al punto di partenza di ogni modifica del reale. E’ fondamentale e indispensabile alla costruzione di qualsiasi teoria.
Non esiste una teoria dell’oggetto senza la sua permanenza, poiché altrimenti tutto apparirebbe come una modifica dello stato dell’oggetto.
Senza permanenza non c’è vera conoscenza. Quale conoscenza dell’oggetto, quale scienza se tutto si modifica e si basa sull’apparenza che tutto si
modifica?

immagine mentale
L’immagine mentale è in qualche sorta una sostituzione interiorizzata dell’oggetto, una imitazione interiorizzata. In questo è prodotto di un atto d’intelligenza. Per Piaget consiste però sempre in una rappresentazione di stati e non di atti (questi figurati solamente come una successione d’immagini statiche). Non funge da strumento di conoscenza, della quale non sarebbe che un significante o simbolo.
L’immagine non è la prolungazione della percezione (del percetto) ma dell’attività di percezione.
L’immagine mentale richiama la distinzione degli aspetti figurativi e degli aspetti operativi della conoscenza (vedi ancora in seguito).

percezione
La percezione è un atto intelligente, è un atto selettivo (delle qualità e di una proprietà che un oggetto può avere ne vengono sempre scelte alcune. Non è un mistero che le ipotesi del soggetto guidino le sue percezioni). Le percezioni non sono elementi indipendenti dall’intelligenza: sono invece un risultato dell’attività intellettuale ²³⁾.
In epistemologia genetica la percezione è considerata sempre come una percezione di schemi e non solamente di oggetti; e la percezione appare anche come una elaborazione o applicazione di schemi, vale a dire come l’organizzazione di dati sensoriali in funzione di un atto o un insieme d’atti.

La visione non é una registrazione meccanica di elementi, ma l’afferrare strutture significanti; la percezione é anche pensiero, ogni ragionamento é anche intuizione, ogni osservazione é anche invenzione. Vedere qualche cosa significa assegnargli il suo posto nel tutto. Se il vedere é afferrare strutture, allora vedere significa scoprire, riscoprire, comprendere o costruire delle strutture. Alla base della percezione sta sempre una ricerca, quindi un atto cognitivo.

ansia (e paura della risposta)
E uno stato di incertezza con prevalenza dei sentimenti di timore. Rispetto l’insegnamento e l’apprendimento come non vedere la paura rispetto le reazioni dell’altro (per esempio di fronte un eventuale errore e la sua ripetizione regolare)? Ma come non vedere l’ansia per qualcosa di sconosciuto, poco chiaro, incompreso (un apprendimento)? Una richiesta (quella del docente) carica di aspettative quanto di pressioni e una incomprensione della domanda? La gestione di una tale carica può essere risolta nella scarica immediata. Oppure c’è la capacità di mantenere il proprio Io in uno stato di indeterminazione, di attesa? La ripetizione di comportamenti acquisiti, una ripetizione generalizzata (coazione a ripetere) anche in maniera non appropriata, deve essere vista come tentativo di scarica dell’ansia. Le risposte date si basano su di:

una scarsa capacità di inventariare le situazioni problema proposte dal docente (la capacità di valutare solo un dato numero ristretto di situazioni è probabilmente associata alla manipolazione “percettiva”, dei problemi (vedi le letture percettive dei problemi, esempio 22);
uno scarso repertorio di risposte possibili.

Tra l’altro in questi casi potremo constatare probabilmente delle reiterate confusioni tra ciò che è possibile e ciò che è necessario ²⁴⁾.

azione e rappresentazione
Piaget parla di rappresentazione e di pensiero a partire dal momento in cui la soluzione dei problemi utilizza la funzione simbolica che aggiunge così un sistema di schemi concettuali agli schemi senso motori.
Con essa si evocano oggetti assenti o azioni non (ancora) eseguite. Per Piaget la rappresentazione comincia solo quando nessun indizio percettivo viene a inficiare la credenza nella permanenza. Tratta della differenza tra significanti e significati.

In psicanalisi (ma non solo) si trova una distinzione fra rappresentazione di cose e rappresentazione di parole. Questa é pure una distinzione evolutiva, nel senso che la rappresentazione di parole é tardiva rispetto la prima.
Se la prima é una traduzione di oggetti in una immagine mentale più o meno fedele, la seconda é già un organizzazione della realtà. Non é una semplice traduzione della realtà, quale potrebbe essere la traccia sonora. Il linguaggio non é una sola traduzione sonora, fonema dopo fonema, di un oggetto, cioè una trascrizione fonetica della realtà. Che dire altrimenti degli avverbi, degli articoli, dei tempi verbali, ecc …

gioco simbolico
Il gioco simbolico si distingue da altre forme come per esempio un gioco senso-motorio o un gioco di regole. L’immagine evocata mentalmente o l’oggetto che sostituisce una classe d’oggetti o d’azioni è sottoposta ad una attività personale, libera e senza limiti o costrizioni. Si definisce per la continuità dell’azione e dell’immaginazione. Il gioco primitivo invece si confonde con le condotte senso-motorie, come attività che non abbisogna di ulteriori accomodamenti e che si riproduce per piacere funzionale.

attività senso-motoria
Attività determinata da stimoli sensoriali, percettivi. Attività che fa intervenire la percezione, le attitudini, il tono e i movimenti. Basata sulla manipolazione di oggetti, invece della parola e dei concetti, utilizza degli schemi di azioni. L’intelligenza senso motoria sa risolvere problemi pratici senza necessità di utilizzare il linguaggio. E’ importante rilevare che questa é una intelligenza pre- verbale. Trae la sua origine tra le esperienze che si fanno prima dell’avvento del linguaggio.

esperienza o attività funzionale
Attività che mette in gioco se stessa.
Lo scopo di una azione non è altro che quello di mettersi in gioco, di fare esperienza della funzione. Si tratta di ripetizioni basate sulla ricognizione dell’atto.

vischiosità
Con questo termine ²⁵⁾si fa riferimento all’impossibilità del soggetto ad abbandonare i dati percettivi nella valutazione di un problema. Il soggetto si manifesta insicuro e altalenante tra due tipi di risposte, una più evoluta dell’altra, senza mai però raggiungere definitivamente e stabilmente il livello superiore. Il soggetto opera delle costruzioni parziali e si cristallizza in stadi intermedi o primari circoscritti. Le attività sono poi poco argomentate, c’é impermeabilità dell’esperienza, vale a dire che il primato percettivo resta difficile da abbandonare. Tutto ciò formerebbe a definire una “mentalità” dove l’operazione mentale non otterrà mai (o solo parzialmente) il primato, rispetto il primato percettivo che non verrà mai a cadere totalmente.

coazione (a ripetere)
Si tratta di fenomeni ripetitivi, (in genere in psicopatologia si parla di atti spiacevoli), della ripetizione di un pensiero o di una azione. Basata sugli istinti è un processo automatico. Il soggetto si pone sistematicamente in una situazione penosa, ripetendo sempre il solito comportamento e dimenticandone il prototipo. L’impressione del soggetto è che la sua risposta sia invece pienamente motivata nella situazione che sta affrontando.

reazioni circolari
Il concetto di reazione circolare tratta della riproduzione attiva di un risultato ottenuto. La ripetizione di una condotta diretta a uno scopo (ottenere un dato effetto o risultato), oppure per mantenere o riscoprire il medesimo risultato (esempio del “fate come me” riportato negli annessi). Si possono differenziare queste reazioni in: primarie, secondarie, terziarie. Le prime trattano della scoperta e conservazione del nuovo senza che ci sia una intenzionalità del soggetto. Il soggetto ripete delle azioni per il piacere di farlo. Le seconde portano interesse ai risultati (non alle azioni) che cercano di ripetere. Le terze sono delle vere e proprie piccole variazioni per vedere “che effetto fa”.
Le reazioni differite implicano invece la memoria. Si tratta di azioni interrotte e poi riprese dal soggetto senza che intervenga più il fattore scatenante.
Per vedere alcune utilizzazioni esplicite delle reazioni circolari vedi allegato A.

reversibilità ed operazioni
La reversibilità è la capacità di compiere una operazione mentale o di svolgere una attività che a questa si colleghi in un senso opposto, ma avendo coscienza che si tratta della stessa cosa. Si parla allora di operazione diretta e di operazione inversa. Ma una operazione è tale proprio perché è coordinata con l’altra e viceversa
La reversibilità vera è la scoperta dell’operazione inversa.
Si distingue dalla rovesciabilità.
L’operazione è una trasformazione coordinata e reversibile da una struttura ad un’altra. E’ tale perché svuotata dalle percezioni.

A questo proposito vorrei rilevare un errore persistente che trova fondamento negli stessi programmi della scuola e nelle definizioni degli algoritmi aritmetici. Sono le stesse quattro operazioni (addizione, sottrazione, moltiplicazione, divisione) ad essere definite in maniera inappropriata. Tutto sono, o possono essere, tranne che delle operazioni.

Tabella A: s- Ragionamenti

S- RAGIONARE: concetti da tenere presente per l’osservazione e la valutazione delle ridondanze di allievi e docenti

– AZIONE – RAPPRESENTAZIONE
– LINGUAGGIO
– SIMBOLICO
– REAZIONI CIRCOLARI
– REVERSIBILITÀ’
– PERMANENZA (dell’oggetto)
– TENTONI
– ANSIA
– COAZIONE A RIPETERE
– ATTIVITÀ’ o ESERCIZIO FUNZIONALE
– MEMORIA
– STADIO

Cosa è che definisce in effetti l’operazione? Come visto certamente la reversibilità. Il fatto, cioè, che a partire da una situazione di partenza poi modificata, io posso tornare all’origine. Pensiamo alle trasformazioni e ai concetti di sostanza, peso o volume, pensiamo alle conservazioni, ecc … il bambino è operatorio quando conserva i concetti ricordati, e quando sul piano logico sa come tornare alla partenza. Eppure i quattro algoritmi aritmetici vengono chiamati operazioni, favorendo la confusione tra la percezione dell’algoritmo, la sua effettuazione e riuscita con il concetto di reversibilità ²⁶⁾.
Ancora una volta si confonde operazione con percezione. Si confonde l’operazione con la rappresentazione di un calcolo. E’ un caso che si definisca come operazione quanto invece è una percezione o una rappresentazione?
Una operazione è definita dalla reversibilità, dunque: se A – B = C allora C – B = A oppure A + B = C

Appare evidente che l’operazione si fa quando il soggetto è in grado di lavorare sulle proprietà e sul ritorno allo stato di partenza.
La vera reversibilità si manifesta quando il soggetto è in grado di svolgere l’operazione inversa.
Il calcolo scritto, magari in colonna, invece non fa che mettere in moto dei pattern di calcolo, di eventuali memorizzazioni di schemi di calcolo, di eventuali disposizioni spaziali delle cifre. Non per nulla, in attività sul valore posizionale delle cifre, molti bambini rispondono conoscendo la posizione delle cifre ma non il valore della posizione.
Un algoritmo non è un operazione. Esso non è che una rappresentazione. Un algoritmo può eventualmente diventare una rappresentazione di una operazione, quando, ben intesi, il soggetto soddisfa alle necessità logiche appena descritte.

pensiero operatorio
In un articolo del 1963 ²⁷⁾ P. Marty – M. De M’Uzan descrivono una dimensione clinica del pensiero che accompagna la malattia psicosomatica: un pensiero senza attività fantasmatica e che accompagna, segue o precede l’azione descrivendola, ma in un lasso temporale limitato.
Senza entrare nei dettagli di ciò che loro hanno chiamato “pensiero operatorio” vediamo che le analogie con un funzionamento percettivo o senso motorio sono molteplici.
E se tale pensiero nulla a che fare con il pensiero operatorio (concreto o formale) di Piaget, dato che la prima accezione concerne una dimensione simbolica e quella di Piaget una dimensione epistemica, curioso è rilevare come la definizione rimane la stessa …
Vediamo brevemente le caratteristiche.
La parola del soggetto non fa che illustrare la situazione, non implica nessuna elaborazione, è fissa sul presente. Pensiero senza associazioni, la sua realtà sta essenzialmente nel fatto che esso non consiste a significare l’azione ma a doppiarla. Il verbo ripete ciò che la mano fa. Attaccato al presente, non permette i benefici che i distacchi temporali della memoria permettono al soggetto, favorendo la fissazione di immagini, simboli, ecc … Smunito di valore libidinale, non permette nemmeno l’esteriorizzazione dell’aggressività. La sua attività si lega principalmente alle cose e non all’immaginazione o alle espressioni simboliche, ciò che suggerisce una scarsa connessione con le parole, almeno al di là del loro aspetto più strettamente descrittivo. Eliminando la distinzione tra significante e significato i due tendono a confondersi . Questo pensiero permette una padronanza solo parziale della realtà, o una pseudo padronanza apparente perché si fonda solo sul controllo della catena delle azioni …
Il termine stesso di “operatorio” suggerisce bene la dimensione del fare, della esecuzione.

Questo è dunque un pensiero retto da un pensiero primario, dove i processi primari sono quelli dominanti rispetto la fantasmatizzazione differita e una elaborazione dell’esperienza.

Processo primario
E’ retto principalmente dalla tendenza alla gratifica immediata (scarica della carica psichica) che è caratteristica di un Io immaturo; caratteristica che domina nettamente l’infanzia e la prima infanzia, ma che rimane sempre presente in tutta la vita. La rappresentazione verbale non viene usata in maniera così esclusiva come nel processo secondario.

Processo secondario
E’ retto principalmente dalla possibilità o dalla capacità di ritardare la scarica energetica. E’ il modo di pensare di un Io relativamente maturo, è retto dal linguaggio e risponde alle leggi della logica e della sintassi

Anche qui le analogie con quanto andiamo descrivendo appaiono numerose e ricche di spunti di riflessione.

stadio
Lo stadio rappresenta una suddivisione dell’evoluzione. Ha una sua struttura e coerenza interna che lo differenziano dagli altri. L’ordine delle acquisizioni é costante e uno stadio precedente viene ad essere inglobato in quello successivo tramite l’integrazione delle strutture

d) figurazione e operazione
Lo sviluppo che porta alla creazione della funzione simbolica (l’immagine mentale ne è una componente come il linguaggio) non si stacca dal lato operatorio. Vale a dire: la figurazione non si sviluppa autonomamente.
L’immagine mentale è uno strumento di conoscenza e dipende dalle funzioni cognitive. Queste si dividono in due distinti aspetti: l’aspetto operatorio e l’aspetto figurativo.
Per Piaget c’é una linea diretta che dalla rappresentazione porta alla rappresentazione, per l’intermediario dell’imitazione. La rappresentazione è la base, lo strumento, la funzione costituente della rappresentazione.
Ci sono tre forme di immagine:

la percezione che funziona esclusivamente in presenza dell’oggetto. Questa non si lancia nell’avventura di modificare l’oggetto;
l’imitazione in senso largo, che funziona in presenza o assenza dell’oggetto ma tramite una riproduzione motoria manifesta. L’imitazione è una copia, più o meno fedele. Un posto importante è quello delle imitazioni differite, vere evocazioni di oggetti assenti;
l’immagine mentale vera e propria, immagine che si manifesta in assenza dell’oggetto. Disegno, figura più o meno schematizzata e interiorizzata. Evidentemente deriva dalla imitazione che ne è un prolungamento. L’immagine nasce con la formazione della funzione simbolica. E’ dunque, per Piaget, il prodotto dell’interiorizzazione delle conoscenze della realtà, ma come copia della realtà, è un simbolo dell’oggetto, una evocazione che tende a figurare un oggetto assente.

Vi è quindi uno sviluppo stadiale che porta dalla percezione all’immagine mentale.

A livello senso motorio possiamo vedere quindi come la percezione può far scattare delle azioni di ricerca o d’attesa di un oggetto (il bebè vedendo la porta che arriva sa che la madre sta per arrivare). Nell’imitazione c’è una schematizzazione di un contenuto (oggetto, individuo, situazione). Così come di fronte a una scheda di calcolo, lo scolaro imita quanto ha visto fare e ha fatto in precedenza, il soggetto prova a dare significato con le proprie azioni a una situazione vissuta od osservata. Gli schemi sono eseguiti precisamente con lo scopo di riprodurre quanto osservato.
Queste azioni sono contemporaneamente significato quando danno una misura della realtà, la indicano o la spiegano; sono significante quando formulano una copia della realtà.

Tipi di lettura di una scheda o di una esperienza

Sequenziale
Rappresentativa
…
Tipi di rappresentazione
1) Testuale
2) Numerica
3) Affettiva
4) Concettuale (visiva)
5) …
6) …
lineare
retroattiva
proattiva
……
C’è poi l’esecuzione motoria dell’esperienza che tende ad eliminare la sua rappresentazione per una esecuzione …

Nell’aritmetica avviene la stessa cosa. Tutto ciò vale anche per il calcolo, la sua tecnica e la sua grafia. Purtroppo negli esempi descritti constatiamo che lo scolaro riproduce gli algoritmi confondendone la natura. Per quegli scolari gli algoritmi sono il significato stesso del calcolo. Confondono il significante con il significato. A scuola danno senso solo alla tecnica, solo alla copia, alla raffigurazione del calcolo (la sua scrittura). La realtà, il significato stesso del calcolo è la sua grafia e l’esecuzione del algoritmo come a sé stante, e non come raffigurazione di una operazione concreta.
Fino ai sette, otto anni il bambino non può produrre che delle immagini “statiche”. Immagini non adatte a figurare movimenti e trasformazioni. Il carattere statico di queste immagini, la loro impossibilità di portare a delle anticipazioni sono strettamente legate alla natura del pensiero pre- operatorio. Sappiamo, per esempio dalle ricerche sulla conservazione, che il bambino centra la sua attenzione sulle configurazioni invece che sulle trasformazioni. Così con la permanenza della sostanza il soggetto si lascerà intrappolare dalla percezione che avrà avuto. Non interessandosi all’azione, il bambino comparerà unicamente le due configurazioni, iniziale e finale.
Questo l’abbiamo ricordato, è il contesto nel quale si manifesta il pensiero pre- operatorio, pensiero statico, senza reversibilità delle operazioni. Il dinamismo dei contenuti, nei contesti cinetici e delle trasformazioni non potrà esser colto.
Questa immagini, seppur interiorizzate, sono dominate dalla propria limitazione intrinseca: servo a copiare, riprodurre. Loro scopo è d’imitare e non costruire o produrre.
Se tali immagini servono a titolo d’informazione o d’archivio, non si può pertanto dire che favoriscono il pensiero. Le immagini legate alla non conservazione della sostanza (livello più alto, più basso, ecc …) non concorrono per nulla alla comprensione di questa trasformazione (che avverrà solo con l’acquisizione della reversibilità).Le immagini d’anticipazione sono possibili con il pensiero operatorio. Queste corrisponderebbero allora a una seriazione di stati successivi, ma solo il pensiero, il linguaggio saprebbe coglierne e descriverne i legami …

Appare costante quindi che sempre la comprensione di una trasformazione o una conservazione come ad esempio 43 + 38 = 81) va al di là della sua immagine. Non è l’immagine che viene a costituire la sua comprensione. La comprensione viene a costruirsi sulle azioni del soggetto.
L’immagine rimane comunque sempre necessaria, perché le conservazioni di una trasformazione si basano comunque sulla percezione di una trasformazione che ha evidentemente due stati. L’uno successivo all’altro. L’immagine fissa poi le conoscenze del soggetto in qualcosa che è trasmissibile … Il confronto contraddittorio di immagini o il confronto d’immagini contraddittorie porta in esso le condizioni ambientali affinché il soggetto abbia a modificare il proprio sguardo sugli avvenimenti.

Una distinzione importante, una frontiera da superare per il soggetto è quella che separa riproduzione o anticipazione dell’immagine. La prima essendo quella che fa resistenza allo sviluppo delle operazioni concrete.
Per vedere uno schema che esplicita una didattica delle rappresentazioni vedi allegato B.

Immagine e linguaggio
L’immagine mentale come il linguaggio è una componente dello sviluppo delle conoscenze e della funzione simbolica. Quali i rapporti fra competenze linguistica e creazione di immagini dunque?
Quante volte il bambino non sa fare uso pertinente del linguaggio? Quante volte sentiamo dire espressioni costruite sui vocaboli “questa cosa”, “questo qui”, “quello là”, ecc … dove l’indicazione non è linguistica ma percettiva (il dito che indica)?

e) sulla natura dell’errore
In età evolutiva bisogna considerare lo squilibrio cognitivo come qualcosa di più che essere solamente legittimo. E la fonte stessa, il motore dell’apprendimento. Senza squilibrio il soggetto non è chiamato a riflettere su nuove modalità di computazione della realtà. L’errore è dunque testimone di una elaborazione ancora insufficiente, che abbisogna di accorgimenti sul piano dell’esperienza e delle sue rappresentazioni.
Questa considerazione è valevole per qualsiasi processo di apprendimento, ma tanto più in età evolutiva – che si definisce da sé – in quanto si riferisce ad un soggetto che si vede trasformare sotto vari aspetti: da quello della maturazione neurologica e biologica, a quello cognitivo ed affettivo, a quello sociale, il bimbo deve ancora superare degli stadi di sviluppo che, in quanto tali, manifestano delle possibilità (residue) e condizioni (limiti) dello stesso.

Ecco alcune dicotomie.

contenuto – processi

Il lavoro sui primi porta sempre a definire un errore, il lavoro sui secondi porta a definire delle modalità come migliori o peggiori, più o meno economiche, più o meno primitive. Ma difficilmente possiamo parlare di errore rispetto una modalità che magari si rivela poco efficace ma che manifesta di un livello specifico di competenza dell’allievo.

esercitazione – test

Molto sovente non c’è uno spazio per la sperimentazione, per i tentativi. Certamente l’esercitazione è da considerare come spazio di apprendimento, ma quante volte è proprio così? Il fatto stesso di negare all’allievo la possibilità di sbagliare sta proprio nella correzione che gli viene proposta.

Per diventare un campione uno sportivo si allena lungamente e duramente, sa che durante l’allenamento può effettuare tutta una serie di esercizi. Durante la gara verrà poi sanzionato, scoprirà quanto vale realmente. Ha uno spazio per l’allenamento e uno per la gara. I due devono essere distinti.

immediatezza – attesa

Un compito, che sia un problema o una scheda di ricupero, esige una risposta, Una esperienza esige una azione (una operazione). Un’azione deve essere svolta (realmente o virtualmente, tramite una rappresentazione mentale) e deve poi essere tradotta in una rappresentazione condivisibile e condivisa. Il lavoro sull’errore si fissa sulla rappresentazione (es. una addizione errata) oppure sulla modalità attuata dal soggetto? Vale a dire guardare come ha fatto il bambino significa posporre la soluzione finita. In questi casi talvolta il pensiero appare bloccato perché si aspetta solamente il risultato da imitare.

paura – tranquillità

E’ innegabile che la risposta elaborata dal soggetto sia caricata di ansia. Ansia per la reazione del docente. Ansia per la gestione della risposta. Si sa che il funzionamento primario tende a delle scariche immediate. Le funzioni della rimozione (affettiva, dinamica) e della memoria cosciente (cognitiva) sono in contrasto. In questo senso il soggetto è legato alla rimozione (della reazione del docente, della vergogna dell’errore, ecc …) e alla non memorizzazione cognitiva dell’esperienza. Non c’è memoria di quanto fatto e la coazione a ripetere é regina in quest’ambito (come spiegare il conteggio 1 a 1 in una addizione tipo 5 + 6 fatta sulle dita ancora in 3a, 4a o 5a elementare?

Accanto a queste dicotomie se ne potrebbero associare sicuramente delle altre. Appare comunque evidente da queste noterelle che la gestione dell’errore richiede una attenzione che non è meccanica. Il lavoro sull’errore non consiste nell’esser recuperato nella sua euristica. Principalmente deve permettere una liberazione della soggettività, del desiderio di sperimentare, della legittimità allo spreco, ecc …

sulla natura dell’errore (2)

Ogni errore del soggetto dovrebbe riferirsi a una competenza che il soggetto stesso mette in opera. Quando il soggetto sta sbagliando corrisponde a un suo processo di “ipotizzazione”, vale a dire se così si comporta é perché gli indizi che lui ha raccolto lo portano a quel tipo di soluzione. E’ ben vero che – data la nostra consegna – raccoglie indizi non pertinenti, ma sono quelli che lui é in grado di raccogliere, sono quelli che lui si permette di raccogliere, quelli, e non altri, che può raccogliere. Il giudizio “é un errore” che é in primo luogo il nostro, non é soggettivamente presente, vale a dire il soggetto può sentirsi più o meno ansioso, più meno bravo, intelligente, diligente, stupido o quant’altro, ma non saprà soggettivamente scoprire spontaneamente il suo errore. Non saprà soggettivamente dire sono in errore.
Quale il suo errore? Per intenderci: quale il suo vero errore, al di là di quello che noi scopriamo nelle sue risposte sbagliate? Quello di aver tentato una soluzione? Quello di essersi esposto alla valutazione del docente? O alla derisione dei compagni?
Non sono pochi gli allievi che rinunciano ad esporsi, abdicando completamente il pensiero, nascondendosi dietro al banco, o chini su di un foglio e non alzando più la mano.

Bambini che non pensano? Quali le possibilità accordate al pensare?
Il pensiero ha delle tappe che devono essere rispettate e queste si fanno (l’abbiamo già visto in precedenza ma lo rammento ancora) per esempio:
sulle conservazioni, sulla riuscita operatoria logico-aritmetica (riuscita logico elementare), sulle conservazioni spaziali, sulle possibilità combinatorie e quindi sulla capacità di coordinare, contemporaneamente un numero maggiore o minore di x di dati e/o di variabili … Ecc…
Oltre il livello epistemologico (più o meno spontaneo) raggiunto dall’allievo negli ambiti scientifici affrontati, dobbiamo capire e scoprire quali sono le capacità di rappresentazione del bambino. E quali sono i blocchi, l’ansia e i fantasmi che reggono il pensiero del bambino …

tipi di errore

non tenere conto del livello operatorio
non tenere conto delle necessità percettive e/o manipolatorie
non tenere conto della potenzialità soggettiva delle rappresentazioni
tipo di lettura che fa il soggetto del testo (vedi tabella precedente)
non individuare dove sta veramente il problema di una situazione
chiedere sempre “cosa hai trovato”, non chiedere “come hai fatto”
……

parte terza

Esperienze

Quale permanenza dell’oggetto se non c’é oggetto?
Quale rappresentazione dell’oggetto (o dell’esperienza) se non c’é esperienza?

domande
Non potrei, e nemmeno desidero farlo, presentare un fantomatico manuale del ragionamento. Non sarei in grado di proporlo, e poi incorrerei nell’errore che si deve evitare: quello di rendere meccaniche e ripetitive delle attività fuori da un contesto, da un processo di ipotizzazione e verifica e così via … Più che dare risposte quello che dobbiamo fare è creare problemi …
Premetto, ripetendomi ancora, come il lavoro da proporre vuole mirare ai modi di processamento del pensiero, alle modalità di computazione del soggetto. Per esempio, dalla percezione degli stati della materia (es. i liquidi, la sostanza), o dalla percezione di configurazioni percettive (il calcolo scritto in colonna) passeremo all’osservazione delle proprie azioni; dalla somministrazione ripetuta di attività e di schede passeremo all’osservazione di quanto stiamo proponendo noi stessi …
E’ poi questo stesso passaggio che regge il salto dalle modalità pre operatorie e senso motorie al pensiero operatorio concreto. Anche se sappiamo che questo salto non è omogeneo e uniforme ma presenta continui décalages, accelerazioni, blocchi ecc …
E’ questo il salto epistemico da svolgere. Una sorta di pedagogia di secondo livello (secondo H. V Foerster) che invece di occuparsi dell’oggetto da apprendere si occupa del soggetto che apprende. Es.: studio d’ambiente o studio del soggetto che studia l’ambiente.
Negli allegati riporto due attività tentate, anche se ciò per i sommi capi. Molti sono però gli esempi ai quali potremmo accedere per sviluppare un intervento sui processi, oppure sui “contenitori” del pensiero: dalle attività di anticipazione, di ascolto e di gestione mentale, alle attività che propongono lo sviluppo della metafora, dalle mappe concettuali, alla decentrazione spaziale, dalla gestione della memoria alla rappresentazione di un compito, dalle attività di argomentazione a quelle di co-costruzione, ecc …

Ricordo come per R. Arnheim (cfr. opere citate) lo sviluppo del pensiero é fortemente legato allo sviluppo e alla comprensione del soggetto di operare delle metafore di natura rappresentativa (visiva) e spaziale ….

Di fronte le difficoltà di ragionamento del bambino si specchiano le difficoltà di ragionamento del docente. Le difficoltà reiterate del bambino sono speculari alla impasse metodologico didattica del docente.
Fare problemi, cosa significa? L’esperienza che il bambino deve svolgere quale deve essere?
Il bambino non sa ragionare? ma quale l’oggetto del suo procedere, quale esperienza di conservazione e di converso di trasformazione della materia? (dove per materia consideriamo la situazione proposta)?

esperienza
L’esperienza: eccolo un termine “onnivoro”, tanto generale quanto fatale.
Il concetto di esperienza rimanda a quello di oggetto.
Avere la permanenza dell’oggetto significa avere avuto ed avere una esperienza dell’oggetto. Ciò tramite delle manipolazioni, il fare delle cose, il fare delle esperienze, avere delle percezioni, visive, cinestetiche, uditive, ecc …
La conoscenza si basa sulle manipolazioni. Da un punto di vista costruttivista ed evolutivo le manipolazioni sono alla base di ogni conoscenza e pure delle sviluppo delle scienze. Con le manipolazioni il soggetto agirà sviluppando raggruppamenti, confronti, modifiche, ecc …

A scuola i concetti di esperienza e di oggetto rimandano a quello dell’insegnamento. Con i bambini che non sanno ragionare quale deve essere l’oggetto dell’insegnamento?
Ecco la domanda: quale permanenza, quale esperienza di permanenza vogliamo sviluppare affinché il bambino abbia ad operare (vale a dire interagire con l’ambiente sulle sue trasformazioni e conservazioni), affinché sia il ragionamento ad essere stimolato? Qual’è l’oggetto d’investimento del docente? Una questione è desiderare la risposta giusta, un’altra desiderare lo sviluppo delle strategie e delle strutture del pensiero ²⁸⁾.
Piaget, per esempio, non era tanto interessato alle risposte quanto alle modalità.

decentramento
L’esperienza di decentramento, fondamentale per lo sviluppo del ragionamento, è centrale. Centrale perché è solo con l’uscita dal modo abituale di procedere che il soggetto è portato a ritrovare altre soluzioni. Purtroppo non è così facile.

In una attività mentale la possibilità di decentrazione del bambino è difficile. Provate a proporgli una prova di spazio proiettivo come quella delle prospettive. Il bambino non saprà dire come un suo compagno vede la disposizione degli oggetti posti su di un ripiano secondo un punto di vista differente al suo. Problema di immagine mentale, di memoria, di esperienza. Come chiedere ad un adulto di descrivere cosa sta dietro ad un palazzo. Se non ci è andato non lo sa. La possibilità di immaginazione è possibile previa una esperienza concreta (tipo il giro del palazzo) finalizzata al compito descritto …

Prendiamo ad esempio il bambino che ad ogni nuovo calcolo deve procedere sempre e comunque con la sola tecnica del conteggio iterativo. Quale è il significato epigenetico di un tale procedere?
Il bambino non è sicuro dell’oggetto, conta uno a uno perché non possiede un “oggetto numerico”. Procede in tal maniera perché l’oggetto del suo procedere, l’oggetto del suo “saper contare” è una grafia, è la grafia stessa del numero (la rappresentazione del numero, la sua scrittura) e non computo di una manipolazione …

Si tratta di ragionare sul tipo di esperienza che si vuole far vivere ad un soggetto. Saper calcolare e scrivere correttamente si rifanno ad una esperienza che non mette in gioco automaticamente una competenza numerica.
Possiamo investire sempre e comunque le competenze percettive, come la grafia di un calcolo, o la corrispondenza di una quantità numerica con la sua traduzione scritta. Oppure le proprietà delle operazioni aritmetiche – come quelle commutativa, transitiva, e invariantiva – possono essere trattate in maniera specifica …

Certamente possiamo trattare delle difficoltà del ragionare in alcuni suoi tratti. Favorendo l’apertura di nuove porte per il bambino, purtroppo non é possibile sostituirsi totalmente e nemmeno in parte alle esperienze dei bambini.
Rimango comunque nella convinzione che qualsiasi pedagogia debba cominciare col riflettere. Ripeto allora che per il docente la prima esperienza in assoluto è sapere e potere sviluppare delle letture di quanto va affrontando. Quanto è stato precedentemente affrontato in maniera generale (vedi concetti, dinamiche ecc …) diventa allora ora un oggetto da investire in maniera specifica. Si tratta quindi di valutare caso per caso l’errore, ipotesi e teorie del soggetto.

ragionare
Torniamo infine all’inizio, all’avvertenza di Bertold Brecht riportata nella premessa, e al mio ammiccare alle “spiegazioni causali”. Per ora mai ho affrontato questo tema. Ma sarebbe l’ora di farlo.
Per ora mi sono limitato ad una lettura critica della quotidianità pedagogica senza mai mettere in discussione il tipo di contenuto offerto al bambino: mi sono lanciato nelle lettura e nella formulazione di ipotesi di intervento rispetto al materiale che tradizionalmente proponiamo ai bambini.
Ho cercato di ipotizzare delle variazioni nella presentazione dei materiali, senza pensare, per ora di modificare i materiali. Mi sono quindi sempre, per ora posto sul terreno dei problemi aritmetici, della lettura di testi, del calcolo, ecc … cioè di quanto a scuola viene codificato come obiettivo di programma, come conoscenza da padroneggiare.
Ho funzionato circolarmente. Sono delle “reazioni circolari” quelle che ho proposto, delle variazioni sullo stesso tema
Tutto ciò era implicito e finché fosse rimasto implicito avrebbe corso il rischio di incorrere – parlo di questa dissertazione – negli errori che vorremmo evitare.
Ma ora si tratta di esplicitare quanto fatto: ma ci si deve sempre e solo muovere nell’ambito di quei contesti scolastici? Ma perché l’esperienza scolastica deve essere quella (solo quella) riportata nei test e nelle schede?
In verità si deve anche pensare se per insegnare il bambino a ragionare dobbiamo limitarci a quei simulacri oppure se non possiamo muoverci su un terreno solo apparentemente totalmente nuovo.
Perché – per favorire delle competenze di ragionamento e delle esperienze cognitive – non ci muoviamo infine in un terreno infinitamente più ricco e che é quello delle relazioni causali? Tutto il pensiero scientifico si costruisce su delle relazioni di causa effetto. E poi tutte le relazioni umane si definiscono sulle medesime dinamiche, sulle relazioni di causa effetto (e sappiamo troppo bene come queste non siano rette da una semplice causalità lineare, quanto piuttosto circolare).

Ma la domanda che ora deve venire sviluppata è la seguente: ma per far ragionare i bambini si devono dare per forza dei problemi aritmetici? Ma i problemi aritmetici favoriscono il ragionamento? Oppure basta dare un problema aritmetico (qualsiasi problema) perché il bambino si metta a ragionare’.
Certamente che no. I problemi aritmetici non favoriscono in maniera generalizzata il ragionamento. Anzi talvolta essi sono presentati poi come una semplice codificazione di una situazione e la soluzione consiste solamente nel cambiare il tipo di codifica (vedi un esempio molto terra a terra allegato).
Certamente: gli ambiti del ragionare sono molto più vasti di quelli aritmetici. Essi investono tutto il campo dell’esperienza, che sia fisica, musicale, intrapersonale, corporea, ecc … ²⁹⁾
E’ questo poi un terreno che é già stato esplorato da Jean Piaget ³⁰⁾ negli inventari. In questa raccolta di schede vengono riportate decine e decine di esperienze scientifiche.

Quanto mi pare importante è la considerazione finale seguente.
Non sono le soluzioni ad essere importanti; ma le domande ben fatte permettono al bambino di sviluppare dei percorsi di ragionamento nei quali possono osservare delle costanti e delle regolarità che siano:
o dell’oggetto studiato – e allora ci muoveremo sul terreno delle conservazioni, del numero dello spazio, della materia, e così via;
o del soggetto che studia – allora ci muoveremo sul terreno delle operazioni mentali e delle sue strutture.

Sono quest’ultimi due aspetti – specialmente il secondo – che spero di sviluppare in un futuro.

Bibliografia + webliografia

AAVV, Inventaires Piagetiens, Les expériences de Jean Piaget, OCDE

J. De Ajuriaguerra, e Altri Organisation psychologique et troubles du développement du language, in, Problèmes psychologiques, PUF, pagg. 109 – 139

R. Arnheim, Arte e percezione visiva, Feltrinelli

R. Arnheim, Pensiero visivo, Einaudi

B. M. Barth, L’apprentissage de l’abstraction, Retz

A.M. Battro, Dictionnaire d’épistémologie génétique, Reidel

C. Bastien, Schèmes et stratégies dans l’activité cognitive de l’enfant, PUF

G. Bateson, Verso una ecologia della mente, Adelphi

G. Bateson, Mente e natura, Adelphi

C. Brenner, Breve corso di psicanalisi, Martinelli

J. Bruner, Verso una teoria dell’istruzione, Armando 1967

A. De La Garanderie, I profili pedagogici, La nuova Italia

B. Douet, Développement des contenants de la pensée, Editions du Centre de Psychologie Appliquée

W. Doise, G. Mugny, La costruzione sociale dell’intelligenza, Il mulino

J. H. Flawell, La mente, dalla nascita all’adolescenza nel pensiero di Jean Piaget, Astrolabio

S. Freud, Formulations sur les deux principes de l’activité psychique

S. Freud, Introduction à la psychanalyse, Payot

G. Galli, L’intelligenza senso-motoria a scuola. Senso motricità e pensiero a scuola. (Alcuni percorsi di ricerca.): P & E, Psicologia & Educazione, rivista dell’Associazione Svizzera di Psicologia dell’Età Evolutiva, 2, 24, 1998, Solothurn, http:// www.ticino.edu/usr/ggalli

G. Galli, Perché il “realismo” ha il sopravvento?, Calicanto, rivista on- line di antropologia dell’educazione e della dominazione, n° 0, http://www.ticino.edu/usr/ggalli/realis.htm

G. Galli, Differenziazione dei programmi e prossimalità dell’apprendimento, P & E, psicologia & Educazione, rivista dell’Associazione Svizzera di Psicologia dell’Età Evolutiva, 2,23, 1997, Solothurn; www.ticino.edu/usr/ggalli/pross.htm

G. Galli, I vestiti dell’imperatore (Il soggetto tra globalizzazione e individuazione) www.ticino.edu/usr/ggalli/vestiti.htm, rivista Calicanto www.ticino.edu/usr/ggalli/calica.htm

M. Gardner, La magie des paradoxes, Pour la science, Belin

H. Gardner, Formae mentis, Feltrinelli

H. Gardner, Educare al comprendere, stereotipi infantili e apprendimento scolastico, Feltrinelli

B. Gibello, L’enfant à l’intelligence troublée, Bayards

T. Gouin Décarie, Intelligence et affectivité chez le jeune enfant, Delachaux et Niestlé

O. Houdé, Catégorisation et développement cognitif, PUF

B. Inhelder, I disturbi dell’intelligenza, Franco Angeli

B. Inhelder – H. Sinclair – M. Bovet, Apprendimento e strutture della conoscenza, Loescher

J. Laplanche – J. B. Pontalis, Enciclopedia della psicoanalisi, 2 vol., Laterza

F. Longeot, Les stades opératoires de Piaget et les facteurs de l’intelligence, Presse Universitaire de Grenoble

F. Marcoli, Il pensiero affettivo, RED

P. Marty – M. De M’Uzan, La “penseée opératoire”, revue Française de Psychanalyse, XXVII, n° spécial, 1963, 345- 356

E. Morin, Introduzione al pensiero complesso, Sperling & Kuiper

E. Morin, La méthode, 4 vol, Seuil

P. Mounoud – A. Guyon- Vinter, Développement cognitif: construction de structures nouvelles ou construction d’organisations internes, Bulletin de psy. 1979, XXXIII, 343, 107- 118

P. Mounoud – A. Guyon- Vinter, Représentation and sensori- motor developpment., In G. Butterworth (ed.), Infancy and Epistemology, Hassocks: Harvester Press, 1981

J. Piaget, La naissance de l’intelligence chez l’enfanT, Delachaux et Niestlé

J. Piaget, Lo sviluppo delle quantità fisiche nel bambino, La nuova Italia

J. Piaget, L’image mentale chez l’enfant, PUF 1966

J. Piaget, La pensée symbolique et la pensée de l’enfant, Arch. de psy. XVIII, 72, 1923, 273- 304

J. Piaget, Le possible et le nécessaire, PUF

J. Piaget, La construction du réel chez l’enfant, Delachaux et Niestlé

J. Piaget, L’équilibration des structures cognitives, PUF

J. Piaget, Recherches sur l’abstraction réfléchissante, 2 vol., PUF

J. Piaget, Les explications causales, PUF

C. Pontecorvo – A. M. Ajello – C. Zucchermaglio, Discutendo si impara, Interazione sociale e conoscenza a scuola, Nuova Italia

A. Techel – A. Pendezzini, La farfalla insegna, la funzione delle emozioni nell’apprendimento, Armando

E. Schmid Kitsikis, L’examen des opérations de l’intelligence, psychopathologie de l’enfant, Delachaux et Niestlé

H. Von Foerster, Disordine/ordine, in: Sistemi che osservano, Astrolabio

P. L. Völzing, La capacità argomentativa nel bambino, Giunti e Barbera

L. Vygotskij, Pensiero e linguaggio, Giunti

H. Wallon, Les origines de la pensée chez l’enfant, PUF

Watzlawick, J. Beavin, D. Jackson, Pragmatica della comunicazione umana, Astrolabio

Watzlawick, J. Weakland, R. Fisch, Change, sulla formazione e la creazione dei problemi, Astrolabio

Watzlawick, Il linguaggio del cambiamento, elementi di comunicazione terapeutica, Feltrinelli

W. Winnicott, Gioco e realtà, Armando

L. Wittgenstein, Ricerche filosofiche, Einaudi

Allegato A

Le tre piccole proposte che presento sono incentrate sulle reazioni circolari. L’esperienza e la sua ripetitività come reazione circolare e come variazione sulle medesime reazioni circolari. Se dovessi farne un commento parlerei di ripetizioni. Ripetere per portare un altro sguardo sulla ripetizione …
Mi muovo decisamente in un ambito tradizionale per quanto riguarda i contenuti

1. la bella ortografia …

Andrea, in classe terza, non presenta particolari e specifiche difficoltà ortografiche. Sbaglia grosso modo quanto i suoi compagni.
Ha una buona competenza fonografica – sa far corrispondere correttamente ogni segno grafico a ogni suono – e sa segmentare le parole. La sua padronanza del codice, in quanto disposizione e capacità di saper far corrispondere suono a segno grafico, é dunque buona
Quando copia un testo, che sia a distanza o ravvicinato, scrive sempre una lettera dopo l’altra, copia lettera dopo lettera, senza mai fissare spezzoni di frase, parole o sillabe. Incede sempre senza mai fissare mentalmente più di un segno grafico per volta. Sovente non copia da sinistra a destra, rispettando il ritmo e la direzionalità della lingua italiana scritta. Copia dall’alto al basso. Vale a dire:

copia la prima lettera a sinistra della prima parola della prima riga,
copia la prima lettera a sinistra della prima parola della seconda riga
copia la prima lettera a sinistra della prima parola della terza riga

e così via di seguito sino ad essere arrivato al fondo del testo

copiando la prima lettera a sinistra della prima parola dell’ultima riga.

Poi ricopia

copia la seconda lettera a sinistra della prima parola della prima riga,
copia la seconda lettera a sinistra della prima parola della seconda riga
copia la seconda lettera a sinistra della prima parola della terza riga

e così via di seguito sino ad essere arrivato al fondo del testo

copiando la seconda lettera a sinistra della prima parola dell’ultima riga.

E poi continua con la terza lettera. Eccetera … copiando quindi non da sinistra a destra ma dall’alto al basso.
Naturalmente in questa maniera non accede mai ai significati, non sa mai cosa sta scrivendo.

intervento
Per informazione dico anche che la grafia, il gesto grafico é curato. Andrea ha una buona calligrafia. Andrea ama anche molto disegnare, specialmente curare i disegni.
Un giorno, per uno specifico progetto pedagogico, la sua classe deve corrispondere in inglese con una classe estera. In effetti la classe di Andrea ha al suo interno alcuni bimbi di lingua madre inglese, ciò non comportava dunque problemi di traduzione e comprensione.
Andrea ricopia le lettere da spedire. Non parla inglese e ricopia due pagine manoscritte in inglese.
Un compito che a noi appare incredibile, improponibile, lo effettua senza obiezioni e senza ulteriori difficoltà.
Ebbene cosa succede?
In questo esercizio di ricopiatura senza senso Andrea si applica talmente, sino (finalmente) scoprire che “Ascona”, il nome della cittadina dove lavoriamo, non necessita di essere ricopiato lettera per lettera “perché so cosa vuol dire” (alla buon ora). Questa la scoperta fatta da Andrea: l’accesso ala senso. L’attività di copiatura può essere un lavoro legato al senso, le parole che copio hanno un senso e posso ricopiarle tenendone a mente uno a o più senza più fissarmi unicamente sui grafemi. Invece di ricordare uno due o tre grafemi ora ricorda una due o tre parole …

2. Dizioni …
prima osservazione
Caterina é impegnata in una lettura.
Legge bene la scheda (una storiella), nel senso che la sua dizione é discreta, il testo relativamente ascoltabile, ecc … Legge forse un po’ in fretta senza avvedersi regolarmente di tutta la punteggiatura.
Normalmente, quando Caterina legge, legge sempre sottovoce, mai mentalmente.
Finita la lettura non sa rispondere a delle domandine. La docente invita la bambina a rileggere. Caterina rilegge per ben due volte, ma non sa rispondere ancora alle domande.

commento

Ciò che ha letto non le pone il problema del significato. Sembrerebbe che per lei “leggere” sia pronunciare ad alta voce i suoni. Non immagina che il testo abbia un significato perché non si pone minimamente il problema che il testo ne possa avere uno.

Per lei leggere significa decodificare.

intervento
Alla bambina viene proposta una scheda assolutamente illeggibile sul piano del significato. Le parole della storia proposta in precedenza sono state tutte rimescolate aleatoriamente.
Dopo una prima scheda gliene propongo una seconda. In questa maniera procede per circa 15 minuti di lettura ad alta voce. Ecco che alla fine di questo “esercizio” a una mia precisa domanda risponde: “Mi é piaciuto, perché le lettere … mi piaceva dire”.

3. ancora dizioni
Ancora Caterina. Questa volta le do due versioni di unmedesimo testo, la prima corretta la seconda con tutte le parole rimescolate in maniera confusa, come descritto in precedenza. La sola differenza percettiva dei due testi sta nella formattazione. Uno occupa più spazio (il teso scompaginato), sembra dunque più lungo. E dice: “questa storia (sig!) era più bella perché più lunga”.

Intervento
Questa volta le do un testo inglese. A Caterina, molto seriamente, faccio leggere un testo scientifico inglese. Tanto, se dovesse persistere nella sua lettura, come atto di unica decodifica, forse non se ne accorgerà?
Dopo un terzo di paginetta circa dice “ma questo non è italiano, non si capisce niente”.

Allegato B

Riporto qui di seguito alcune proposte che per ora sono state descritte nel documento di lavoro“3 interventi attorno a: “astrazione, simbolizzazione e operatività aritmetica” , e che per ora non ha avuto una divulgazione più larga.

Allegato C – schemini

rappresentazioni
Lavoro sulle rappresentazioni per andare oltre le rappresentazioni, confronto sulle rappresentazioni per scoprirne le costanze e le equivalenze ecc …
Dalla esecuzione della soluzione alla percezione delle soluzioni …
Dalla percezione della soluzione alla percezione delle modalità interne…
Questo é lo schema di un percorso ripetuto e ripetibile …

1	AZIONE	Fare il camion Giocare il camion
2	RAPPRESENTAZIONE	Disegnare il camion (progettare, nominare) Chi progetta il camion, chi nomina le parti chi, nomina il materiale necessario, ecc …
3	RAPPRESENTAZIONE DELLA RAPPRESENTAZIONE O RAPPRESENTAZIONE ²(di secondo livello)	Guardare, confrontare, discutere i vari camion 1, camion 2, … camion n, disegnati dai vari bambini o dallo stesso bambino Serve per dire: “ma tu come hai fatto?” e non per guardare le differenti rappresentazioni. Il lavoro sulle rappresentazioni deve portare sulle modalità interne che le hanno prodotte, il confronto delle rappresentazioni deve in effetti servire per confrontare le modalità, le azioni mentali che le hanno prodotte, e non le immagini. Le immagini servono per quello scopo, altrimenti non servono. Il lavoro sulle immagini (le rappresentazioni) serve se porta a riflettere sulle modalità, altrimenti non vale nemmeno la pena farlo.

In questo percorso ciò che é interessante é:
– vedere la varie rappresentazioni (fase 3 o rappresentazione di secondo livello)
– confrontare queste rappresentazioni con problemi analoghi
– fare una rappresentazione collettiva delle rappresentazioni precedenti (o rappresentazione di un terzo livello) che sicuramente comporterà soluzioni molto più astratte

Aiutare a ragionare

A) Individuare l’errore, leggere l’errore

L’errore corrisponde ad una rappresentazione, a una idea, una ipotesi, una modalità di trattazione dei dati e di tradurli in un altro linguaggio

tipo di codifica della situazione	relazione della codifica con l’esperienza
codifica verbale codifica aritmetica codifica affettiva codifica scientifica	azione gioco

tipo di codifica del docente e dell’allievo

B) partire dai differenti tipi di rappresentazione e fare un confronto:

percettivo: qual’è la soluzione, il risultato
operatorio: cosa ho fatto
ciò eventualmente spinge a un confronto percettivo

C) lavoro sulla soluzione

lavoro sulle modalità,

Domande tipo:

cosa hai trovato

come hai fatto

domande

Bambini che non pensano dunque:

2 modi di valutare la questione:

A) interna al soggetto, le possibilità interiori che il bambino possiede;
B) esterna, del ambiente, della classe o della programmazione didattica: quali possibilità vengono accordate al pensare del bambino?

Domande:
1. Quali sono le possibilità del pensare che soggettivamente si dà il soggetto (blocchi, ansia, ecc …) o che semplicemente possiede il soggetto?

2. Quali le possibilità da un punto di vista evolutivo ed epistemico?
3. Quali sono le sue competenze di visualizzare, cioè creare immagini corrette?

Punto due, facciamo un breve esempio.
Il pensiero ha delle tappe (e delle esigenze). Queste tappe si fanno:

sulle conservazioni,
sulle riuscite logico aritmetiche,
sulle possibilità combinatorie,

ciò determina la quantità e la qualità di dati e variabili che posso coordinare.

condizioni

Ogni errore di lettura si riferisce ad una competenza, ad una riuscita operatoria che il soggetto non ha ancora potuto costruire.

Es.:

confusione tra valore e marca
mancata padronanza della seriazione
mancata padronanza dell’inclusione di classe
mancata padronanza della combinatoria
mancata padronanza delle conservazioni
……

La domanda diventa quindi: quale la competenza che non appare?

Vi sono almeno 5 condizioni che portano alla ridondanza di un errore. Queste condizioni possono essere dello scolaro come della situazioneproposta. Sono quindi limitazioni interne al soggetto o limitazioni esterne al soggetto, vale a dire limitazioni dell’impostazione del problema da parte del docente…

il tipo di problema (la situazione) permette di ragionare
la competenza linguistica, le lettura del testo (competenza semantica, padronanza del codice, ecc …)
possibilità soggettive (ansia, blocchi, fatica, perseveranza …)
livello operatorio
capacità rappresentative simboliche

Nota: il riferimento è sempre agli errori di ragionamento. Non trattiamo invece quelli di computazione,

Allegato D

Esempi di problemi senza ragionamento
(fare una trascodifica è un ragionamento?)

Ragionare = tessere delle relazioni, fare delle ipotesi, verificare le variabili …

Un problema del tipo 43 + 53.

Facevo la spesa . Ho speso 43.- franchi per alimenti vari. Poi ho ancora speso 53.- fr. per una camicetta. Quanto ho speso?

Ebbene non é un problema. Ma solo una rappresentazione o una codifica. All’allievo non chiede di fare altro che di tras-codificare quanto scritto in un calcolo

NOTE

1) Cfr. “L’intelligenza senso-motoria a scuola. Senso motricità e pensiero a scuola.(Alcuni percorsi di ricerca)“: P & E, Psicologia & Educazione, rivista dell’Associazione Svizzera di Psicologia dell’Età Evolutiva, 2, 24, 1998, Solothurn (torna)

2) Cfr. nota precedente. (torna)

3) A proposito delle intelligenze multiple cfr. ad esempio i due testi di H. Gardner citati in bibliografia; sulla molteplicità dei percorsi operatori cfr. F. Longeot, Les stades opératoires de Piaget et les facteurs de l’intelligence, Presse Universitaire de Grenoble; per quanto riguarda lo sviluppo cognitivo come ritorno a condotte ri-attualizzate vedi P. Mounoud – A. Guyon-Vinter, Développement cognitif: construction de structures nouvelles ou construction d’organisations internes, Bulletin de psy. 1979, XXXIII, 343, 107-118; sui décalages cfr. ad esempio J. Piaget, Lo sviluppo delle quantità fisiche nel bambino, La nuova Italia; sul concetto di viscosità vedi B. Inhelder, I disturbi dell’intelligenza, Franco Angeli. (torna)

4) Si potrà obiettare che la costruzione di questa corrispondenza rivela dalla comprensione, ed è dunque un atto intelligente. Certo, anche la permanenza dell’oggetto primario, come pure l’apprendimento della guida dell’automobile sono frutto di un atto d’intelligenza. Ma è un dato di fatto che è una conoscenza senso motoria e che deve manifestarsi nella sua automaticità, come un arco riflesso, ci mancherebbe che l’autista debba pensare a tutte le operazioni che sta facendo e che deve fare quando deve frenare bruscamente per evitare un incidente! Certamente: una buona padronanza, una buona meccanica libera il soggetto ad altri compiti … Ma è proprio questa “meccanica non liberata” ad occuparci, questa impossibilità del soggetto a muoversi oltre la meccanica.
Prendiamo pure anche come esempio la lettura di un testo straniero: non dobbiamo certamente più preoccuparci del come si pronuncia, ma tutto ciò avviene per automatismi …
Oppure prendiamo lo stesso atto dello scrivere: l’attività redazionale si divide certamente in una parte ortografica e un’altra di senso, di trasmissione di informazioni e/o d’esperienze … (torna)

5) Troppo sovente si dice dell’allievo che non é motivato, che é un lazzarone, ecc … Ciò che si deve considerare e capire é che per l’allievo é molto più difficile sopportare l’onta dell’insuccesso, oppure gestire la rabbia del propria non riuscita che non la “gloria” dovuta alla buona risposta. Se solo potesse vorrebbe ben essere un allievo modello. Non si diverte certamente ad essere lo zimbello del gruppo e del docente … (torna)

6) E’ interessante rilevare come vengono considerati i contenuti cosiddetti trasversali nei programmi della scuola. Questi sono intravisti nello studio d’ambiente. Temi come “l’acquedotto comunale”, “il bosco”, “la castagna, “l’inverno”, ecc … vengono quindi a stimolare l’allievo favorendo l’applicazione delle competenze di lettura, scrittura, calcolo, ecc … arricchendone sicuramente il bagaglio enciclopedico dell’allievo. A questi contenuti omogenei impostati dal docente per tutta la classe si aggiungono poi oggi le “ricerche” personali quali il “capolavoro” al fine di favorire maggiormente l’interesse del singolo allievo e la differenziazione pedagogico didattica.
E’ interessante però rilevare come in questi ambiti tutto sia ancora di sapore “enciclopedico”. Trattiamo ancora di conoscenze non di processi. A questo livello favoriamo lo sviluppo di conoscenze legate all’ambiente vissuto e sicuramente importanti per la comprensione del territorio nel quale si vive. Favoriamo pure una applicazione, come detto, di competenze computazionali.
Eppure … Perché lo studio d’ambiente deve sempre essere fisico-geografico? Perché non può per esempio essere musicale oppure logico aritmetico? Perché un tema come quello delle “Strutture” non vede la luce? Eppure la nostra vita, il nostro ambiente è pieno di strutture che meritano un’analisi …
Oppure “Analogie, astrazioni, simulazioni” …
Il considerare le analogie che ci sono fra modi di pensare in ambiti professionali differenti non sono forse, non potrebbero forse essere oggetto di uno studio d’ambiente? L’ambiente si definisce unicamente per le nozioni che gli allievi sono obbligati ad ingurgitare oppure l’ambiente si definisce anche e soprattutto per le operazioni che svolgiamo con esso e su di esso? (torna)

7) Per una definizione interessante dei copioni cfr. H. Gardner, Educare al comprendere, stereotipi infantili e apprendimento scolastico, Feltrinelli (torna)

8) H. Von Foerster, Percezione del futuro e futuro della percezione, in Sistemi che osservano, pag. 129-130. (torna)

9) Giovanni Galli, “Perché il “realismo” ha il sopravvento?, Calicanto, rivista on-line di antropologia dell’educazione e della dominazione, n° 0, (torna)

10) Fra le attività più significative a tal riguardo ci sono i cosiddetti problemi aritmetici (oggi chiamati anche situazioni). La maggior parte delle volte, nel miglior dei casi si tratta di situazioni facsimile, non reali problemi, poiché la soluzione già c’é. Banalizzazioni di attività quotidiane, quali fare la spesa, salire su di un autobus, giocare a palla … totalmente scollegate dalle esperienze e motivazioni dei bambini. Il fatto poi che siano scritti e che molto raramente vengano realizzati come una esperienza concreta non deve meravigliarci se poi vengono affrontati e risolti con una “lettura percettiva” o una modalità percettiva di risoluzione dei problemi. (torna)

11) R. Arnheim tratta in un modo molto interessante lo sviluppo della percezione in ambito artistico. In arte e percezione visiva, propone dei modelli di tipo gestaltistico relativi allo sviluppo delle competenze pittoriche … (torna)

12) “Quella che sembra essersi imposta in quasi tutto il mondo della scuola é una distensione sterile. Gli insegnati chiedono agli studenti di risolvere certi problemi prefissati, di appropriarsi di liste i termini, di memorizzare e di riformulare, a richiesta, le definizioni”, H. Gardner, Educare al comprendere, Feltrinelli, pag. 158. “Le scuole hanno optato dovunque non già per i “rischi del comprendere”, ma per il “compromesso delle risposte corrette”, op. cit. pag. 150 (torna)

13) Cfr. ad es. De la Garanderie (torna)

14) L. Wittgenstein, in Ricerche filosofiche, tratta mirabilmente delle funzioni della parola, del linguaggio e della comunicazione. Parola, lingua non sono sinonimi di comunicare e di pensare (torna)

15) H. Von Foerster, op. cit. pag. 172 (torna)

16) Le ragioni di questo fatto sono molteplici. In particolare vorrei qui ricordare come la scuola proponga poche esperienze concrete, non é un laboratorio o solamente raramente é un laboratorio. Ma non può nemmeno credersi onnipotente e sostituirsi alle esperienze che mancano dei suoi allievi. Da un punto di vista epistemico si può affermare che la scuola non viene a favorire nuove esperienze per i suoi soggetti quanto a darne un ordine convenzionale … (torna)

17) Senza entrare nel dettaglio vediamo subito come le due situazioni estreme, cioè quella ++ e quella — possono essere le migliori definite (?). Sono queste le situazioni di bambini con un QI alto con una buona strutturazione, soggetto dotati e che godono e hanno goduto di adeguati aiuti e stimoli casalinghi; e quella di bambini con un QI basso e una strutturazione bassa. Ci muoviamo qui in un ambito di deprivazione e di pseudo debilità.
Le altre due +-, -+ sono quelle meno chiare.La prima quella di bambini con un QI alto ma con una strutturazione bassa, richiama la situazione di soggetti immaturi, con deficit cognitivo ma drillati, condizionati, infarinati di nozioni “enciclopediche”. Questi in genere si trovano piuttosto bene a scuola e la scuola non si avvede del loro ritardo cognitivo.
La seconda quella dei bambini con un QI basso con una buona strutturazione richiama i soggetti deprivati culturalmente e socialmente. Sono bambini che paradossalmente sovente vengono bocciati. Sono le prime vittime nelle scuole dell’ignoranza praticata e concretizzata relative alle strutture del ragionamento.
Per una mia breve trattazione dei pericoli della differenziazione in atto nelle scuole vedi i miei articoli: Differenziazione dei programmi e prossimalità dell’apprendimento, P & E, psicologia & Educazione, rivista dell’Associazione Svizzera di Psicologia dell’Età Evolutiva, 2,23, 1997, Solothurn; I vestiti dell’imperatore (Il soggetto tra globalizzazione e individuazione), (torna)

18) A questo proposito cfr. ancora il testo precedente. (torna)

19) Cfr. Watzlawick, J. Weakland, R. Fisch, Change, sulla formazione e la creazione dei problemi, Astrolabio (torna)

20) Bisogna considerare e ricordare che l’errore è frutto dell’azione dell’allievo. Sovente vediamo l’allievo come passivo, così lo descriviamo, ma l’allievo è proprio attivo e sovente a fronte di una sua passività ricettiva (nell’ascolto della lezione) è attivo nelle risposte (seppur erronee) che dà. (torna)

21) Sul concetto di vischiosità cfr. il testo di B. Inhelder, I disturbi dell’intelligenza, edito da Franco Angeli. (torna)

22) Ajuriaguerra, Guignard, Jäggi, Kocher, Maquard, Paunier, Qinodoz, Siotis, Organisation psychologique et troubles du développement du language, in, Problèmes psychologiques, PUF, pagg. 109 – 139.(torna)

23) Cfr. J. Piaget, La construction du réel chez l’enfant, Delachaux et Niestlé (torna)

24) Cfr. J. Piaget, Le possible et le nécessaire, PUF (torna)

25) Cfr. l’interessante lavoro di B. Inhelder op. cit. (torna)

26) Da non confondere con la rovesciabilità … (torna)

27) P. Marty – M. De M’Uzan, La “penseée opératoire”, revue Française de Psychanalyse, XXVII, n° spécial, 1963, 345-356 (torna)

28) Cfr. per esempio l’interessante testo di Gibello dove dimostra che accanto a buoni risultati al QI nel Wechsler possono esistere gravi difficoltà nel ragionamento in soggetti che presentano delle regressioni o fissazioni disarmoniche nello sviluppo delle strutture cognitive (lui le chiama “i contenenti del pensiero”, assieme a una debole coerenza interna di queste stesse strutture. (torna)

29) H.Gardener, in Educare al comprendere, tratta della (non) trattazione a scuola delle diverse forme di intelligenza da lui descritte in Formae mentis. (torna)

30) Cfr., AAVV, Inventaires Piagetiens, Les expériences de Jean Piaget, OCDE (torna)